题目内容
9．
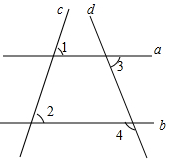直线a、b、c、d的位置如图所示，如果∠1=58°，∠2=58°，∠3=70°，那么∠4等于110°．
分析 根据同位角相等，两直线平行这一定理可知a∥b，再根据两直线平行，同旁内角互补即可解答．
解答 
解：∵∠1=∠2=58°，
∴a∥b，
∴∠3+∠5=180°，
即∠5=180°-∠3=180°-70°=110°，
∴∠4=∠5=110°，
故答案为：110°．
点评 本题主要考查了平行线的判定和性质，对顶角相等的运用，熟记定理是解题的关键．解题时注意：同位角相等，两直线平行．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
4．在△ABC和△DEF中，AB=DE，∠B=∠E，如果补充一个条件后不一定能使△ABC≌△DEF，则补充的条件是（ ）
| A． | BC=EF | B． | ∠A=∠D | C． | AC=DF | D． | ∠C=∠F |
14．有下列命题：
①两条直线被第三条直线所截，同位角相等；
②0.1 的算术平方根是0.01；
③算术平方根等于它本身的数是1；
④如果点P（3-2n，1）到两坐标轴的距离相等，则n=1；
⑤若a2=b2，则a=b；
⑥若$\root{3}{a}$=$\root{3}{b}$，则a=b．
其中假命题的个数是（ ）
①两条直线被第三条直线所截，同位角相等；
②0.1 的算术平方根是0.01；
③算术平方根等于它本身的数是1；
④如果点P（3-2n，1）到两坐标轴的距离相等，则n=1；
⑤若a2=b2，则a=b；
⑥若$\root{3}{a}$=$\root{3}{b}$，则a=b．
其中假命题的个数是（ ）
| A． | 3个 | B． | 4 个 | C． | 5个 | D． | 6个 |
18．若a=-32，b=-3-2，c=（-$\frac{1}{3}$）-2，d=（-$\frac{1}{3}$）0，则它们的大小关系是（ ）
| A． | a＜b＜c＜d | B． | b＜a＜d＜c | C． | a＜d＜c＜b | D． | c＜a＜d＜b |