题目内容
20.如果不等式组$\left\{\begin{array}{l}{\frac{x}{2}+a-\frac{b}{2}>2}\\{2x+a+2b<3}\end{array}\right.$的解集是1<x<2,求:坐标原点到直线y=ax+b距离.分析 根据不等式组$\left\{\begin{array}{l}{\frac{x}{2}+a-\frac{b}{2}>2}\\{2x+a+2b<3}\end{array}\right.$的解集是1<x<2,得到关于a,b的二元一次方程组$\left\{\begin{array}{l}{-2a+b+4=1}\\{\frac{-a-2b+3}{2}=2}\end{array}\right.$,解方程组得到a,b的值,再根据互相垂直的两条直线的关系可得经过原点并且与直线y=ax+b垂直的直线解析式,联立两直线解析式可得交点坐标,再根据勾股定理即可求解.
解答 解:$\left\{\begin{array}{l}{\frac{x}{2}+a-\frac{b}{2}>2①}\\{2x+a+2b<3②}\end{array}\right.$,
解①得x>-2a+b+4,
解②得x<$\frac{-a-2b+3}{2}$,
∵不等式组$\left\{\begin{array}{l}{\frac{x}{2}+a-\frac{b}{2}>2}\\{2x+a+2b<3}\end{array}\right.$的解集是1<x<2,
∴2a+b+4=1,
解②得x<$\frac{-a-2b+3}{2}$,
∴$\left\{\begin{array}{l}{-2a+b+4=1}\\{\frac{-a-2b+3}{2}=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$,
∴直线y=ax+b的解析式为y=x-1,
∴经过原点并且与直线y=ax+b垂直的直线解析式为y=-x,
联立两解析式$\left\{\begin{array}{l}{y=x-1}\\{y=-x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$,
由勾股定理可得坐标原点到直线y=ax+b距离为$\sqrt{(\frac{1}{2})^{2}+(-\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$.
点评 考查了一次函数与一元一次不等式,互相垂直的两条直线的关系,勾股定理,方程思想,解题的关键是得到a,b的值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | a4•a5=a20 | B. | x8÷x2=x4 | C. | (a3)2=a9 | D. | (3a2)2=9a4 |
| A. |  | B. |  | C. |  | D. |  |
 遗爱湖公园的亲水平台修建了许多台阶(如图所示),春季湖水上涨后有一部分在水下.如果点C的坐标为(-1,1),D点的坐标为(0,2).(点C、D分别在第3、4级)
遗爱湖公园的亲水平台修建了许多台阶(如图所示),春季湖水上涨后有一部分在水下.如果点C的坐标为(-1,1),D点的坐标为(0,2).(点C、D分别在第3、4级)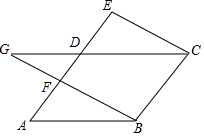 如图,在?ABCD中,AD=4,AB=5,延长AD到点E,连接EC过点B作BF∥CE交AD于点F,交CD的延长线于点G.
如图,在?ABCD中,AD=4,AB=5,延长AD到点E,连接EC过点B作BF∥CE交AD于点F,交CD的延长线于点G.