题目内容
6．关于x的一元二次方程x2+（m-2）x-2m=0有两个相等的实数根，则m的值是（ ）| A． | -2 | B． | 2 | C． | 4+±$\sqrt{2}$ | D． | 0或8 |
分析 由方程有两个相等的实数根结合根的判别式即可得出△=（m+2）2=0，解之即可得出结论．
解答 解：∵关于x的一元二次方程x2+（m-2）x-2m=0有两个相等的实数根，
∴△=（m-2）2-4×1×（-2m）=m2+4m+4=（m+2）2=0，
解得：m=-2．
故选A．
点评 本题考查了根的判别式，牢记“当△=0时，方程有两个相等的实数根”是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．
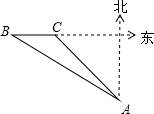如图，海关缉私艇在A处接到情报，在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行，于是该艇立即沿北偏西45°的方向前进，经过1小时航行，恰好在C处截住可疑船只，则缉私艇的速度为（ ）
如图，海关缉私艇在A处接到情报，在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行，于是该艇立即沿北偏西45°的方向前进，经过1小时航行，恰好在C处截住可疑船只，则缉私艇的速度为（ ）| A． | （12$\sqrt{2}$+12$\sqrt{6}$）海里/时 | B． | （12$\sqrt{3}$+12$\sqrt{6}$）海里/时 | C． | （12$\sqrt{2}$+12$\sqrt{3}$）海里/时 | D． | （8$\sqrt{3}$+8$\sqrt{6}$）海里/时 |
11．某班开展以“提倡勤俭节约，反对铺张浪费”为主题教育活动．为了解学生每天使用零花钱的情况，小明随机调查了10名同学，结果如下表：
关于这10名同学每天使用的零花钱，下列说法正确的是（ ）
| 每天使用零花钱（单位：元） | 0 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 2 | 4 | 1 | 2 |
| A． | A、平均数是3 | B． | 中位数是4 | C． | 众数是2 | D． | 方差是4 |
18．
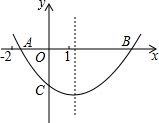二次函数y=ax2+bx+c的图形如图，OA=OC，下列结论：①abc＜0；②4ac＜b2；③ac-b＜-1；④ac-2a+1＞0；⑤OB•OC=-$\frac{c}{a}$．其中结论正确的序号有（ ）
二次函数y=ax2+bx+c的图形如图，OA=OC，下列结论：①abc＜0；②4ac＜b2；③ac-b＜-1；④ac-2a+1＞0；⑤OB•OC=-$\frac{c}{a}$．其中结论正确的序号有（ ）| A． | ②⑤ | B． | ②④⑤ | C． | ②③④⑤ | D． | ②③⑤ |
16．若代数式$\frac{x}{x+2}$在实数范围内有意义，则x的取值范为是（ ）
| A． | x≥-2 | B． | x≠2 | C． | x≠0 | D． | x≠-2 |