题目内容
9．已知一个样本1，3，2，x，4的平均数是3，则这个样本的方差是（ ）| A． | 2 | B． | 2.5 | C． | 10 | D． | $\frac{6}{5}$ |
分析 根据平均数的定义先求出x的值，再根据方差公式进行计算即可．
解答 解：∵样本1，3，2，x，4的平均数是3，
∴（1+2+3+4+x）÷5=3，
解得：x=5，
则这个样本方差s2=$\frac{1}{5}$[（1-3）2+（2-3）2+（3-3）2+（4-3）2+（5-3）2]=2．
故选A．
点评 此题考查了方差，一般地设n个数据，x1，x2，…xn的平均数为$\overline{x}$，则方差S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
20．把多项式3x2+y3-5xy2-x3，按x的升幂排列正确的是（ ）
| A． | y3-5xy2+3x2-x3 | B． | -x3+3x2-5xy2+y3 | C． | y3+5xy2+3x2+x3 | D． | 5xy2+3x2-x3+y3 |
4．关于x的方程x2+kx-1=0的根的情况描述正确的是（ ）
| A． | k为任何实数，方程都没有实数根 | |
| B． | k为任何实数，方程都有两个不相等的实数根 | |
| C． | k为任何实数，方程都有两个相等的实数根 | |
| D． | 根据 k 的取值不同，方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
1．
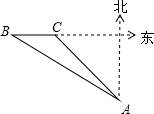如图，海关缉私艇在A处接到情报，在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行，于是该艇立即沿北偏西45°的方向前进，经过1小时航行，恰好在C处截住可疑船只，则缉私艇的速度为（ ）
如图，海关缉私艇在A处接到情报，在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行，于是该艇立即沿北偏西45°的方向前进，经过1小时航行，恰好在C处截住可疑船只，则缉私艇的速度为（ ）| A． | （12$\sqrt{2}$+12$\sqrt{6}$）海里/时 | B． | （12$\sqrt{3}$+12$\sqrt{6}$）海里/时 | C． | （12$\sqrt{2}$+12$\sqrt{3}$）海里/时 | D． | （8$\sqrt{3}$+8$\sqrt{6}$）海里/时 |
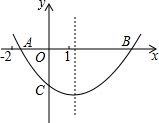二次函数y=ax2+bx+c的图形如图，OA=OC，下列结论：①abc＜0；②4ac＜b2；③ac-b＜-1；④ac-2a+1＞0；⑤OB•OC=-$\frac{c}{a}$．其中结论正确的序号有（ ）
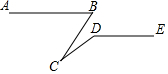如图，∠D=140°，当∠B与∠C满足∠B+∠BCD=140°时，AB∥DE．