题目内容
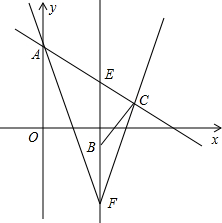 如图,已知点A(0,6),B(4,-2),C(7,
如图,已知点A(0,6),B(4,-2),C(7,| 5 |
| 2 |
(1)求证:∠CFE=∠AFE;
(2)在y轴上是否存在这样的点P,使△AFP与△FBC相似?若有,请求出所有符合条件的点P的坐标;若没有,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得AC、FC的解析式,根据自变量的值,可得函数值,根据函数值,可得相应自变量的值,根据SAS,可得三角形全等,根据全等三角形的性质,可得答案;
(2)根据两直线平行,可得内错角相等,根据等量代换,可得∠PAF=∠BFC,根据两边对应成比例,夹角相等的两个三角形相似,可得答案.
(2)根据两直线平行,可得内错角相等,根据等量代换,可得∠PAF=∠BFC,根据两边对应成比例,夹角相等的两个三角形相似,可得答案.
解答:(1)证明:过点A作AM∥x轴,交FC于点M,交BE于点N.
∴AN=4.
设直线AC的解析式为y=k1x+b1,
则有
,解得
.
∴直线AC的解析式为y=-
x+6
当x=4时,y=-
×4+6=4
∴点E的坐标为(4,4),
∵点F与E关于点B对称,则点F的坐标为(4,-8)
设直线FC的解析式为y=k2x+b2,
则有
,解得
.
∴直线FC的解析式为y=
x-22
∵AM与x轴平行,则点M的纵坐标为6.
当y=6时,则有
x-22=6,
解得x=8.
∴AM=8,MN=AM-MN=4,
∴AN=MN,
∵FN⊥AM,
∴∠ANF=∠MNF=90°.
在△ANF和△MNF中,
∴△ANF≌△MNF (SAS)
∴∠CFE=∠AFE.
(2)解:∵C的坐标为(7,
),F坐标为(4,-8)
∴CF=
=
又∵A的坐标为(0,6),
∴FA=
=2
,
又∵BF=6,
∵EF∥AO,则有∠PAF=∠AFE,
又由(2)可知∠BFC=∠AFE,
∴∠PAF=∠BFC.
①若△AFP1∽△FCB,
则
=
,即
=
,解得P1A=8.
∴OP1=8-6=2,
∴P1的坐标为(0,-2).
②若△AFP2∽△FBC,
则
=
,即
=
,解得P2A=
.
∴OP2=6-
=-
,
∴P2的坐标为(0,-
).
所以符合条件的点P的坐标有两个,分别是P1(0,-2),P2(0,-
).
∴AN=4.
设直线AC的解析式为y=k1x+b1,

则有
|
|
∴直线AC的解析式为y=-
| 1 |
| 2 |
当x=4时,y=-
| 1 |
| 2 |
∴点E的坐标为(4,4),
∵点F与E关于点B对称,则点F的坐标为(4,-8)
设直线FC的解析式为y=k2x+b2,
则有
|
|
∴直线FC的解析式为y=
| 7 |
| 2 |
∵AM与x轴平行,则点M的纵坐标为6.
当y=6时,则有
| 7 |
| 2 |
解得x=8.
∴AM=8,MN=AM-MN=4,
∴AN=MN,
∵FN⊥AM,
∴∠ANF=∠MNF=90°.
在△ANF和△MNF中,
|
∴△ANF≌△MNF (SAS)
∴∠CFE=∠AFE.
(2)解:∵C的坐标为(7,
| 5 |
| 2 |
∴CF=
(
|
3
| ||
| 2 |
又∵A的坐标为(0,6),
∴FA=
| (6+8)2+42 |
| 53 |
又∵BF=6,
∵EF∥AO,则有∠PAF=∠AFE,
又由(2)可知∠BFC=∠AFE,
∴∠PAF=∠BFC.
①若△AFP1∽△FCB,
则
| P1A |
| BF |
| AF |
| CF |
| P1A |
| 6 |
2
| ||||
|
∴OP1=8-6=2,
∴P1的坐标为(0,-2).
②若△AFP2∽△FBC,
则
| P2A |
| CF |
| AF |
| BF |
| P2A | ||||
|
2
| ||
| 6 |
| 53 |
| 2 |
∴OP2=6-
| 53 |
| 2 |
| 41 |
| 2 |
∴P2的坐标为(0,-
| 41 |
| 2 |
所以符合条件的点P的坐标有两个,分别是P1(0,-2),P2(0,-
| 41 |
| 2 |
点评:本题考查了一次函数的综合题,(1)待定系数法求解析式,全等三角形的性质得出答案;(2)分类讨论PA与BF对应边,PF与CF是对应边,以防漏掉.

练习册系列答案
相关题目
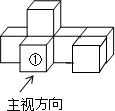 如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )| A、主视图改变,俯视图改变 |
| B、左视图改变,俯视图改变 |
| C、俯视图不变,左视图改变 |
| D、主视图不变,左视图不变 |
已知四组线段的长分别如下,以各组线段为边,能组成三角形的是( )
| A、l,3,4 | ||||
| B、1,2,5 | ||||
C、1,2,
| ||||
D、1,
|
 如图,⊙O1和⊙O2外切于点P,O1 O2的延长线交⊙O2于点A,AB切⊙O1于点B,交⊙O2于点C.BE是⊙O1的直径,连结PE,过点B作BF⊥O1P,垂足为F,延长BF交PE于点G,连结BP.
如图,⊙O1和⊙O2外切于点P,O1 O2的延长线交⊙O2于点A,AB切⊙O1于点B,交⊙O2于点C.BE是⊙O1的直径,连结PE,过点B作BF⊥O1P,垂足为F,延长BF交PE于点G,连结BP.