题目内容
20.计算①3$\sqrt{2}$+4$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{3}$
②($\sqrt{18}$-$\sqrt{12}$+$\sqrt{2}$)×2$\sqrt{6}$
③$\sqrt{15}$×$\frac{3}{5}$$\sqrt{20}$÷(-$\frac{1}{3}$$\sqrt{6}$)
④(7+4$\sqrt{3}$)(7-4$\sqrt{3}$)-($\sqrt{5}$-1)2.
分析 ①合并同类二次根式即可;
②先把二次根数化为最简二次根式,再根据乘法的分配律进行计算即可;
③先把二次根数化为最简二次根式,再利用二次根式的乘除法进行计算即可;
④根据平方差公式和完全平方公式进行计算即可.
解答 解:①原式=$\sqrt{2}$+5$\sqrt{3}$;
②原式=(3$\sqrt{2}$-2$\sqrt{3}$+$\sqrt{2}$)×2$\sqrt{6}$
=(4$\sqrt{2}$-2$\sqrt{3}$)×2$\sqrt{6}$
=16$\sqrt{3}$-12$\sqrt{2}$;
③原式=$\sqrt{15}$×$\frac{3}{5}$×2$\sqrt{5}$×(-$\frac{3}{\sqrt{6}}$)
=-9$\sqrt{2}$;
④原式=1-(6-2$\sqrt{5}$)
=2$\sqrt{5}$-5.
点评 本题考查了二次根式的混合运算,在二次根式的混合运算中,要掌握好运算顺序及各运算律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列图形:线段、角、圆、平行四边形、矩形、正方形中,既是轴对称图形又是中心对称图形的有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
3.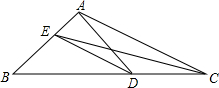 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
 如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )
如图,在△ABC中,点D是BC上的一点,已知∠DAC=30°,∠DAB=75°,CE平分∠ACB交AB于点E,连接DE,则∠DEC=( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
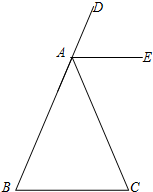 如图,△ABC中,AB=AC,AE是外角∠DAC的角平分线.
如图,△ABC中,AB=AC,AE是外角∠DAC的角平分线. 若二次函数y=ax2+bx+c的图象如图所示,则它的对称轴是x=3.
若二次函数y=ax2+bx+c的图象如图所示,则它的对称轴是x=3.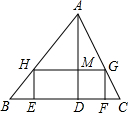 如图,在△ABC中,AD是高,矩形EFGH的顶点H、G分别在AB、AC上,EF在BC上,AD与HG的交点为M.若BC=40cm,AD=30cm,且HG=2HE.则矩形EFGH的周长为72cm.
如图,在△ABC中,AD是高,矩形EFGH的顶点H、G分别在AB、AC上,EF在BC上,AD与HG的交点为M.若BC=40cm,AD=30cm,且HG=2HE.则矩形EFGH的周长为72cm.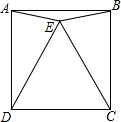 如图,四边形ABCD是正方形,△CDE是等边三角形,若AE=4cm,则S△AEB=4cm2.
如图,四边形ABCD是正方形,△CDE是等边三角形,若AE=4cm,则S△AEB=4cm2.