题目内容
13.一个正多边形的内角和等于1440°,则此多边形是10边形,它的每一个外角是36°.分析 先设该多边形是n边形,根据多边形内角和公式列出方程,求出n的值,即可求出多边形的边数,再根据多边形的外角和是360°,利用360除以边数可得外角度数.
解答 解:设这个多边形的边数为n,则
(n-2)×180°=1440°,
解得n=10.
外角:360÷10=36,
故答案为:10;36°.
点评 此题考查了多边形的内角与外角,关键是根据多边形的内角和公式(n-2)•180°和多边形的外角和都是360°进行解答.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
8.二次函数的部分对应值如下表:
由图可知该二次函数的图象对称轴为x=1,x=2对应的函数值y=-8.
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | 5 | 7 | … |
18.纳米是一种长度单位,1纳米=10-9米.已知某种花粉的直径为35000纳米,则用科学记数法表示该花粉的直径为( )
| A. | 3.5×10-6m | B. | 3.5×10-5m | C. | 35×10-4m | D. | 3.5×104m |
2.若x=-2,则x0、x-1、x-2之间的大小关系是( )
| A. | x0>x-2>x-1 | B. | x-2>x-1>x0 | C. | x0>x-1>x-2 | D. | x-1>x-2>x0 |
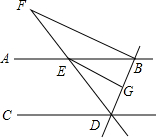 如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥DB,垂足为B,EG平分∠DEB,∠CDE=50°,∠F=25°.
如图,直线AB,CD被直线BD,DF所截,AB∥CD,FB⊥DB,垂足为B,EG平分∠DEB,∠CDE=50°,∠F=25°. 如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=5米,则坝底AC的长度是5$\sqrt{3}$米.
如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=5米,则坝底AC的长度是5$\sqrt{3}$米.