题目内容

12．如图，以直角三角形①的三边为边向外作正方形，再分别以所得的两个小正方形的边作斜边向外作直角三角形②、③，再分别以直角三角形②、③的直角边为边向外作正方形，若直角三角形①的斜边长为2，则图中所有正方形的面积为12．

分析 根据勾股定理可得AB2+AC2=BC2=4，进而可得以BC为边的正方形面积为4，以AB、AC为边的两个正方形面积和为4，再根据勾股定理可得FD2+EF2=DE2，KM2=MN2+KN2，进而可得FD2+EF2+MN2+KN2=4，从而可得答案．

解答 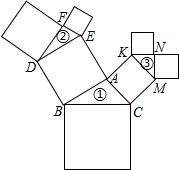解：∵直角三角形①的斜边长为2，
∴AB2+AC2=BC2=4，
∴以BC为边的正方形面积为4，以AB、AC为边的两个正方形面积和为4，
∵AB2+AC2=4，
∴DE2+KM2=4，
∵②③是直角三角形，
∴FD2+EF2=DE2，KM2=MN2+KN2，
∴FD2+EF2+MN2+KN2=4，
∴所有正方形的面积为：4×3=12，
故答案为：12．

点评 此题主要考查了勾股定理，关键是掌握直角三角形两直角边的平方和等于斜边的平方．

练习册系列答案
相关题目
2．解方程：
（1）（x-1）（x+2）=2（x+2）
（2）2x2-5x-3=0．
3．某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究
（1）如图1，△ABC两内角∠ABC与∠ACB的平分线交于点E．则∠BEC=90°+$\frac{1}{2}$∠A．
（阅读下面证明过程，并填空．）
理由：∵BE、CE分别平分∠ABC和∠ACB，
∴∠EBC=$\frac{1}{2}$∠ABC，∠ECB=$\frac{1}{2}$∠ACB（角平分线的性质）　
∴∠BEC+∠EBC+∠ECB=180°（三角形内角和定理）
∴∠BEC=180°-（∠EBC+∠ECB）
=180°-（ $\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB）=180°-$\frac{1}{2}$（∠ABC+∠ACB）
=180°-$\frac{1}{2}$（180°-∠A）
=180°-90°+$\frac{1}{2}$∠A=90°+$\frac{1}{2}$∠A
（2）如图2，△ABC的内角∠ABC的平分线与△ABC的外角∠ACM的平分线交于点E．
请你写出∠BEC与∠A的数量关系，并说明理由．
答：∠BEC与∠A的数量关系式：∠A=2∠BEC．
理由：
∵BE是∠ABC的平分线，CE是∠ACM的平分线，
∴∠EBC=$\frac{1}{2}$∠ABC，∠ECM=$\frac{1}{2}$∠ACM．
∵∠ACM是△ABC的外角，∠ECM是△BCE的外角，
∴∠ACM=∠A+∠ABC，∠ECM=∠BEC+∠EBC，
∴，∠ECM=$\frac{1}{2}$∠ACM=$\frac{1}{2}$（∠A+∠ABC）=∠BEC+∠EBC，即$\frac{1}{2}$∠A+∠EBC=∠BEC+∠EBC，
∴∠A=2∠BEC．．
（3）如图3，△ABC的两外角∠CBD与∠BCF的平分线交于点E，请你直接写出∠BEC与∠A的数量关系，不需证明．
20．若多项式x3+ax2+bx能被x-5和x-6整除，则a=-11，b=30．
7．一元二次方程x2=x的根是（　　）
A．x=1B．x=0C．x1=x2D．x1=0，x2=1
17．如图所示，已知AD∥EF∥BC，FG∥CH，且DF=2CF．
（1）求AE：BE的值．
（2）当CH=6时，求FG的长．
4．把下列多项式分解因式：
（1）12x3y2z-9x2yz+3xyz；
（2）2a（x-3）+4a（3-x）2．
1．如图，有A，B两家酒店去年下半年的月营业额折线统计图．
（1）要评价两家酒店7-12月营业额的平均水平，你选择什么统计量？求出这个统计量；
（2）分别求出两家酒店7-12月的月营业额的方差；
（3）根据（1），（2）两题的结果和折线统计图，你认为哪家酒店经营状况较好？请简述理由．
2．如图，在△ABC中，∠ABC和∠BAC的角平分线交于点O，OD⊥BC，OE⊥AC，OF⊥AB，垂足分别为D、E、F．  OC平分∠ACB吗？为什么？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网