题目内容
16. 如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.
如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.(1)求证:直线DE是⊙O的切线;
(2)若 BF=10,sin∠BDE=$\frac{{\sqrt{5}}}{5}$,求DE的长.
分析 (1)先连接OD,根据∠ODB=∠DBE,即可得到OD∥AC,再根据DE⊥AC,可得OD⊥DE,进而得出直线DE是⊙O的切线;
(2)先连接DF,根据题意得到∠F=∠BDE,在Rt△BDF中,根据$\frac{BD}{BF}$=sinF=sin∠BDE=$\frac{\sqrt{5}}{5}$,可得BD=2$\sqrt{5}$,在Rt△BDE中,根据sin∠BDE=$\frac{BE}{BD}$=$\frac{\sqrt{5}}{5}$,可得BE=2,最后依据勾股定理即可得到DE的长.
解答  解:(1)如图所示,连接OD,
解:(1)如图所示,连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD平分∠OBC,
∴∠OBD=∠DBE,
∴∠ODB=∠DBE,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵OD是⊙O的半径,
∴直线DE是⊙O的切线;
(2)如图,连接DF,
∵BF是⊙O的直径,
∴∠FDB=90°,
∴∠F+∠OBD=90°,
∵∠OBD=∠DBE,∠BDE+∠DBE=90°,
∴∠F=∠BDE,
在Rt△BDF中,$\frac{BD}{BF}$=sinF=sin∠BDE=$\frac{\sqrt{5}}{5}$,
∴BD=10×$\frac{\sqrt{5}}{5}$=2$\sqrt{5}$,
∴在Rt△BDE中,sin∠BDE=$\frac{BE}{BD}$=$\frac{\sqrt{5}}{5}$,
∴BE=2$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=2,
∴在Rt△BDE中,DE=$\sqrt{B{D}^{2}-B{E}^{2}}$=$\sqrt{16}$=4.
点评 本题主要考查了切线的判定以及解直角三角形的运用,解决问题的关键是作辅助线,构造等腰三角形以及直角三角形,解题时注意:经过半径的外端且垂直于这条半径的直线是圆的切线.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案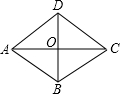 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )| A. | 当AB=BC时,平行四边形ABCD是菱形 | |
| B. | 当AC⊥BD时,平行四边形ABCD是菱形 | |
| C. | 当AC=BD时,平行四边形ABCD是正方形 | |
| D. | 当∠ABC=90°时,平行四边形ABCD是矩形 |
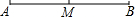 如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )
如图,点M在线段AB上,则下列条件不能确定M是AB中点的是( )| A. | BM=$\frac{1}{2}$AB | B. | AM+BM=AB | C. | AM=BM | D. | AB=2AM |
| A. | x<3 | B. | x≥2 | C. | 2≤x<3 | D. | 2<x<3 |
| A. | 13 | B. | $\frac{240}{13}$ | C. | 120 | D. | $\frac{120}{13}$ |
 如图所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O经过4次旋转而得到,则每一次旋转的角度大小为72°.
如图所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O经过4次旋转而得到,则每一次旋转的角度大小为72°. 将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合,当α最小时,点A运动的路径长为$\frac{2π}{3}$.
将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合,当α最小时,点A运动的路径长为$\frac{2π}{3}$.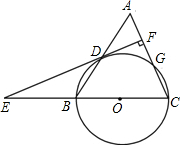 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.