题目内容
1．不等式组$\left\{\begin{array}{l}{x-1＜2}\\{2x≥4}\end{array}\right.$的解集为（ ）| A． | x＜3 | B． | x≥2 | C． | 2≤x＜3 | D． | 2＜x＜3 |
分析 先求出每个不等式的解集，再求出不等式组的解集即可．
解答 解：$\left\{\begin{array}{l}{x-1＜2①}\\{2x≥4②}\end{array}\right.$
∵解不等式①得：x＜3，
解不等式②得：x≥2，
∴不等式组的解集为2≤x＜3，
故选C．
点评 本题考查了解一元一次不等式组，能根据不等式的解集求出不等式组的解集是解此题的关键．
练习册系列答案
相关题目
11．下列二次根式中不能够与$\sqrt{2}$合并的是（ ）
| A． | $\sqrt{8}$ | B． | -$\sqrt{\frac{1}{2}}$ | C． | $\sqrt{12}$ | D． | $\sqrt{18}$ |
12．下列计算正确的是（ ）
| A． | $\sqrt{8}$÷2=$\sqrt{2}$ | B． | （2$\sqrt{2}$）2=16 | C． | 2×$\sqrt{\frac{3}{2}}$=$\sqrt{3}$ | D． | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ |
如图，BF为⊙O的直径，直线AC交⊙O于A，B两点，点D在⊙O上，BD平分∠OBC，DE⊥AC于点E．
6．
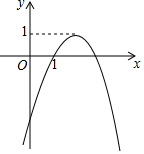在平面直角坐标系xOy中，二次函数y=ax2+bx+c（a≠0）的大致图象如图所示，则下列结论正确的是（ ）
在平面直角坐标系xOy中，二次函数y=ax2+bx+c（a≠0）的大致图象如图所示，则下列结论正确的是（ ）| A． | a＜0，b＜0，c＞0 | |
| B． | -$\frac{b}{2a}$=1 | |
| C． | a+b+c＜0 | |
| D． | 关于x的方程ax2+bx+c=-1有两个不相等的实数根 |
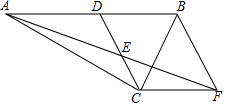已知：如图，在Rt△ACB中，∠ACB=90°，点D是AB的中点，点E是CD的中点，过点C作CF∥AB交AE的延长线于点F．