题目内容
14.已知关于x的一元二次方程x2+(2m-1)x+m2+3=0(1)若方程有两个实数根,求m的取值范围;
(2)若方程有两个实数根x1,x2,且x12+x22=25,求m的值.
分析 (1)由方程有实数根即可得出△=-4m-11≥0,解之即可得出m的取值范围;
(2)根据根与系数的关系可得出x1+x2=-(2m-1)、x1•x2=m2+3,结合x12+x22=25即可得出关于m的一元二次方程,解之即可得出m的值,再由(1)中m的取值范围即可确定m的值.
解答 解:(1)∵关于x的一元二次方程x2+(2m-1)x+m2+3=0有两个实数根,
∴△=(2m-1)2-4×1×(m2+3)=-4m-11≥0,
解得:m≤-$\frac{11}{4}$.
∴m的取值范围为m≤-$\frac{11}{4}$.
(2)∵方程x2+(2m-1)x+m2+3=0的实数根为x1,x2,
∴x1+x2=-(2m-1),x1•x2=m2+3.
又∵x12+x22=(x1+x2)2-2x1•x2=25,
∴[-(2m-1)]2-2(m2+3)=25,
解得:m1=-3,m2=5.
∵m≤-$\frac{11}{4}$,
∴m的值为-3.
点评 本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)牢记“当△≥0时,方程有实数根”;(2)由根与系数的关系结合x12+x22=25,找出关于m的一元二次方程.

练习册系列答案
相关题目
4.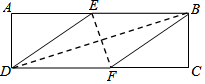 在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
②若DE2=BD•EF,则DF=2AD,则( )
 在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )
| A. | ①是假命题,②是假命题 | B. | ①是真命题,②是真命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①是真命题,②是假命题 |
9.在一次数学测验中,随机抽取了8份试卷,其得分如下表:
则这8名考生得分的中位数是86分.
| 得分 | 80 | 85 | 87 | 90 |
| 人数 | 1 | 3 | 2 | 2 |
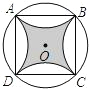 如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π.
如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π. 如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADE交BC于点F.若BD⊥EF,请判断四边形EBFD是什么四边形,并说明理由.
如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADE交BC于点F.若BD⊥EF,请判断四边形EBFD是什么四边形,并说明理由.
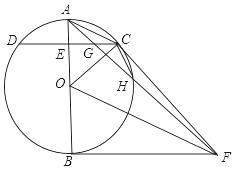 如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连结AF,FC,AF与CD交于点G,与⊙O交于点H,连结CH.
如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连结AF,FC,AF与CD交于点G,与⊙O交于点H,连结CH.