题目内容
12.在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是( )| A. | 4:3 | B. | 3:4 | C. | 16:9 | D. | 9:16 |
分析 根据角平分线的性质,可得出△ABD的边AB上的高与△ACD的AC上的高相等,估计三角形的面积公式,即可得出△ABD与△ACD的面积之比等于对应边之比.
解答 解:∵AD是△ABC的角平分线,
∴设△ABD的边AB上的高与△ACD的AC上的高分别为h1,h2,
∴h1=h2,
∴△ABD与△ACD的面积之比=AB:AC=4:3,
故选A.
点评 本题考查了角平分线的性质,以及三角形的面积公式,熟练掌握三角形角平分线的性质是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
20.已知2m=3,3m=2,则6m等于( )
| A. | 1 | B. | 1.5 | C. | 5 | D. | 6 |
17.下列运算正确的是( )
| A. | 6ab÷2a=3ab | B. | (2x2)3=6x6 | C. | a2•a5=a7 | D. | a8÷a2=a4 |
4.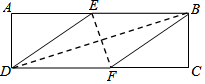 在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
②若DE2=BD•EF,则DF=2AD,则( )
 在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )
| A. | ①是假命题,②是假命题 | B. | ①是真命题,②是真命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①是真命题,②是假命题 |
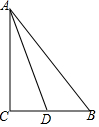 已知,如图,在△ABC中.∠C=90°,AD平分∠BAC.
已知,如图,在△ABC中.∠C=90°,AD平分∠BAC.