题目内容
6.已知x2-3x+1=0,求$\sqrt{\frac{3{x}^{3}+2{x}^{2}+3x}{{x}^{4}-3{x}^{2}+1}}$的值.分析 由题意x+$\frac{1}{x}$=3,故x2+$\frac{1}{{x}^{2}}$=7,根号下的式子分子、分母都除以x2,利用整体代入的思想解决.
解答 解:∵x2-3x+1=0,
∴x+$\frac{1}{x}$=3,
∴x2+$\frac{1}{{x}^{2}}$=7,
∴原式=$\sqrt{\frac{3(x+\frac{1}{x})+2}{{x}^{2}+\frac{1}{{x}^{2}}-3}}$=$\sqrt{\frac{9+2}{7-3}}$=$\sqrt{\frac{11}{4}}$=$\frac{\sqrt{11}}{2}$.
点评 本题考查分式、二次根式的求值问题以及整体代入的数学思想,把x2-3x+1=0转化为x+$\frac{1}{X}$=-3是解决问题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
16.下列各数中,为有理数的是( )
| A. | π | B. | $\sqrt{3}$ | C. | 3.14 | D. | $-\sqrt{3}$ |
17.下列四个实数中无理数的是( )
| A. | 0 | B. | $\sqrt{16}$ | C. | $\frac{22}{7}$ | D. | π |
4. 如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=2BD,则$\frac{CF}{CB}$的值为( )
如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=2BD,则$\frac{CF}{CB}$的值为( )
 如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=2BD,则$\frac{CF}{CB}$的值为( )
如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=2BD,则$\frac{CF}{CB}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |

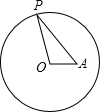 如图,点A在半径为3的⊙O内,OA=$\sqrt{3}$,P为⊙O上一点,当∠OPA取最大值时,PA的长等于$\sqrt{6}$.
如图,点A在半径为3的⊙O内,OA=$\sqrt{3}$,P为⊙O上一点,当∠OPA取最大值时,PA的长等于$\sqrt{6}$.