题目内容
11．
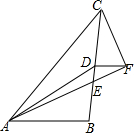如图，AD，AE分别是△ABC的中线和角平分线，作CF⊥AE的延长线于点F．若AB=2，AC=6，则DF的长为2．
分析 延长AB、CF相交于点G，根据等腰三角形三线合一的性质判断出AG=AC，CF=FG，然后判断出DF是△BCG的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半可得DF=$\frac{1}{2}$BG解答．
解答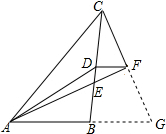 
解：如图，延长AB、CF相交于点G，
∵AE是△ABC的角平分线，CF⊥AE，
∴AG=AC，CF=FG，
又∵AD是△ABC的中线，
∴CD=BD，
∴DF是△BCG的中位线，
∴DF=$\frac{1}{2}$BG，
∵AB=2，AC=6，
∴BG=AG-AB=AC-AB=6-2=4，
∴DF=$\frac{1}{2}$×4=2．
故答案为：2．
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半，等腰三角形的判定与性质，难点在于作辅助线构造出以DF为中位线的三角形．
练习册系列答案
阅读快车系列答案
相关题目
如图是一个3×3的方格，请你把-1，2，-3，4，-5，6，-7，8，-9分别填在这些方格中，使每行、每列、对角线上的三个数的乘积都是负数．
已知：BE=DE，BE⊥DE，AE=DC，且DC⊥AC，求证：△ABE≌△CED．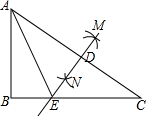
如图所示，在Rt△ABC中，∠B=90°，∠C=30°，分别以A、C为圆心，大于$\frac{1}{2}$AC长为半径画弧，两弧相交于点M、N，连接MN，与AC、BC分别交于点D、E，连接AE
如图，将一矩形OABC放在直角坐标系中，O为坐标原点，点A在y轴正半轴上，点E是边AB上的一个动点（不与点A、B重合），过点E的一次函数y=kx+b的图象与边BC交于点F，交y轴于点P（0，3），若OA=2，OC=4．