题目内容
3. 如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的一次函数y=kx+b的图象与边BC交于点F,交y轴于点P(0,3),若OA=2,OC=4.
如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的一次函数y=kx+b的图象与边BC交于点F,交y轴于点P(0,3),若OA=2,OC=4.(1)若△OAE、△OCF的面积分别为S1、S2.且S1•S2=4,求k和b的值;
(2)在(1)的条件下,写出直线OE、OF的函数解析式.
分析 (1)把P坐标代入一次函数解析式求出b的值;根据矩形OABC边OA的长确定出E的纵坐标;根据OC的长求出F的横坐标,分别代入一次函数解析式表示出AE与CF,进而表示出三角形OAE与三角形OCF的面积,代入S1•S2=4求出k的值即可;
(2)由(1)确定出E与F坐标,即可确定出直线OE与直线OF解析式.
解答 解:(1)把P(0,3)代入y=kx+b中得:b=3,即一次函数解析式为y=kx+3,
由题意得:E纵坐标为2,F横坐标为4,
把y=2代入一次函数解析式得:x=-$\frac{1}{k}$;把x=4代入一次函数解析式为y=4k+3,
即AE=-$\frac{1}{k}$,CF=4k+3,
∴S1=$\frac{1}{2}$×2×(-$\frac{1}{k}$)=-$\frac{1}{k}$,S2=$\frac{1}{2}$×4×(4k+3)=8k+6,
代入S1•S2=4得:-8-$\frac{6}{k}$=4,即k=-$\frac{1}{2}$,
则k=-$\frac{1}{2}$,b=3;
(2)根据(1)得:E(2,2),F(4,1),
则直线OE解析式为y=x;直线OF解析式为y=$\frac{1}{4}$x.
点评 此题考查了一次函数综合题,涉及的知识有:坐标与图形性质,矩形的性质,待定系数法求一次函数解析式,熟练掌握一次函数性质是解本题的关键.

练习册系列答案
相关题目
 求图中阴影部分的面积.
求图中阴影部分的面积.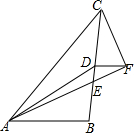 如图,AD,AE分别是△ABC的中线和角平分线,作CF⊥AE的延长线于点F.若AB=2,AC=6,则DF的长为2.
如图,AD,AE分别是△ABC的中线和角平分线,作CF⊥AE的延长线于点F.若AB=2,AC=6,则DF的长为2.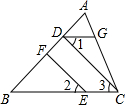 如图,CD⊥AB于D,E是BC上一点,EF⊥AB于F,∠1=∠2.试说明∠BDG+∠B=180°.
如图,CD⊥AB于D,E是BC上一点,EF⊥AB于F,∠1=∠2.试说明∠BDG+∠B=180°.