题目内容
10.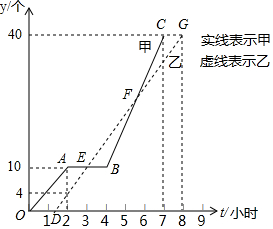 某车间甲、乙两名工人分别生产同种零件,他们生产的零件数量y(个)与生产时间t(小时)之间的关系如图所示(其中实线表示甲,虚线表示乙,且甲因机器故障停产了一段时间).
某车间甲、乙两名工人分别生产同种零件,他们生产的零件数量y(个)与生产时间t(小时)之间的关系如图所示(其中实线表示甲,虚线表示乙,且甲因机器故障停产了一段时间).(1)甲、乙中,甲先完成40个零件的生产任务.
(2)甲在因机器故障停产之前,每小时生产5个零件.
(3)甲故障排除之后以原来速度的两倍重新开始生产,则甲停产了2小时.
(4)在第一次甲乙生产零件总数在同一时刻相同到甲完工这段时间,什么时候甲乙生产的零件总数相差3个?
分析 (1)根据图象可以的到甲、乙完成40个零件的时间;
(2)根据图象得出甲的生产速度即可;
(3)计算甲完成剩余30个零件的生产任务需要用时,根据总时间即可得;
(4)根据函数图象求出两函数解析式,再分类讨论即可得.
解答 解:(1)由图象知,甲在t=7时完成生产任务,而乙在t=8时完成生产任务,
故答案为:甲;
(2)∵10÷2=5(个/小时),
∴甲在因机器故障停产之前,每小时生产5个零件,
故答案为:5;
(3)由题意知,甲完成剩余30个零件的生产任务需要用时(40-10)÷10=3(小时),
∴甲停产时间为7-2-3=2(小时),
故答案为:2;
(4)当2≤t≤4时,y=10;
当4<t≤7时,设y=kt+b,
将(4,10)、(7,40)代入,得:$\left\{\begin{array}{l}{4k+b=10}\\{7k+b=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=10}\\{b=-30}\end{array}\right.$,
∴y=10t-30,
即y甲=$\left\{\begin{array}{l}{10}&{(2≤t≤4)}\\{10t-30}&{(4<t≤7)}\end{array}\right.$,
设y乙=mt+n,
将(2,4)、(8,40)代入,得:$\left\{\begin{array}{l}{2m+n=4}\\{8m+n=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=6}\\{n=-8}\end{array}\right.$,
∴y乙=6t-8,
①若6t-8-10=3,解得t=$\frac{7}{2}$;
②若6t-8-(10t-30)=3,解得t=$\frac{19}{4}$;
③若(10t-30)-(6t-8)=3,解得t=$\frac{25}{4}$;
综上,t=$\frac{7}{2}$、$\frac{19}{4}$、$\frac{25}{4}$时,甲乙生产的零件总数相差3个.
点评 此题主要考查了一次函数的应用,根据题意得出函数关系式以及数形结合是解决问题的关键.

| A. | 3-(2-3)=2 | B. | 2(2a-b)-3(b-2a)=10a-5b | ||
| C. | 6÷($\frac{1}{2}$-$\frac{1}{3}$)=12-18=-6 | D. | (-4)2-$\root{3}{-8}$=14 |
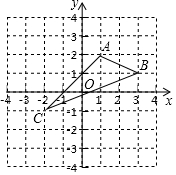 如图,在平面直角坐标系中
如图,在平面直角坐标系中