题目内容
关于x的一元二次方程mx2-(2m-1)x+m-2=0(m>0)
(1)求证:此方程有两个不相等的实数根;
(2)如果这个方程的两个实数根分别为x1,x2,且(x1-3)(x2-3)=5m,求m的值.
(1)求证:此方程有两个不相等的实数根;
(2)如果这个方程的两个实数根分别为x1,x2,且(x1-3)(x2-3)=5m,求m的值.
考点:根的判别式,根与系数的关系
专题:证明题
分析:(1)先根据判别式的值得到△=4m+1,由m>0得到△>0,则根据判别式的意义得到此方程有两个不相等的实数根;
(2)根据根与系数的关系得x1+x2=
,x1•x2=
,由(x1-3)(x2-3)=5m变形得到x1•x2-3(x1+x2)+9=5m,所以
-3•
+9=5m,
整理得5m2-4m-1=0,解方程得m1=-
(舍去),m2=1,所以m=1.
(2)根据根与系数的关系得x1+x2=
| 2m-1 |
| m |
| m-2 |
| m |
| m-2 |
| m |
| 2m-1 |
| m |
整理得5m2-4m-1=0,解方程得m1=-
| 1 |
| 5 |
解答:(1)证明:△=(2m-1)2-4m(m-2)
=4m+1,
∵m>0,
∴4m+1>0,
∴此方程有两个不相等的实数根;
(2)解:根据题意得x1+x2=
,x1•x2=
,
∵(x1-3)(x2-3)=5m,
∴x1•x2-3(x1+x2)+9=5m,
∴
-3•
+9=5m,
整理得5m2-4m-1=0,解得m1=-
,m2=1,
而m>0,
∴m=1.
=4m+1,
∵m>0,
∴4m+1>0,
∴此方程有两个不相等的实数根;
(2)解:根据题意得x1+x2=
| 2m-1 |
| m |
| m-2 |
| m |
∵(x1-3)(x2-3)=5m,
∴x1•x2-3(x1+x2)+9=5m,
∴
| m-2 |
| m |
| 2m-1 |
| m |
整理得5m2-4m-1=0,解得m1=-
| 1 |
| 5 |
而m>0,
∴m=1.
点评:本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了根与系数的关系.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 如图,小正方体的棱长为1,求对角线AG的长.
如图,小正方体的棱长为1,求对角线AG的长.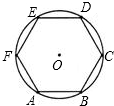 如图,已知正六边形ABCDEF的外接圆半径R=8cm,求四边形ABDE的面积.
如图,已知正六边形ABCDEF的外接圆半径R=8cm,求四边形ABDE的面积. 如图,已知D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,求∠B的度数.
如图,已知D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,求∠B的度数.