题目内容
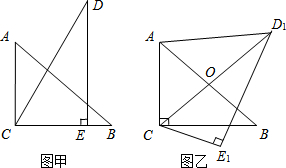 把一副三角板如图甲放置,其中AB=6,DC=7,∠ACB=∠DEC=90°,∠A=45°,∠D=30°,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为
把一副三角板如图甲放置,其中AB=6,DC=7,∠ACB=∠DEC=90°,∠A=45°,∠D=30°,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为考点:旋转的性质
专题:计算题
分析:由∠ACB=∠DEC=90°,∠A=45°,∠D=30°得到∠DCE=60°,△ABC为等腰直角三角形,再根据旋转的性质得∠D1CE1=∠DCE=60°∠BCE1=15°,所以•∠D1CB=45°,于是可判断OC为等腰直角三角形ABC斜边上的中线,则OC⊥AB,OC=OA=
AB=3,则OD=CD-OC=4,然后在Rt△AOD1中根据勾股定理计算AD1.
| 1 |
| 2 |
解答:解:∵∠ACB=∠DEC=90°,∠A=45°,∠D=30°
∴∠DCE=60°,△ABC为等腰直角三角形,
∵三角板DCE绕着点C顺时针旋转15°得到△D1CE1,
∴∠D1CE1=∠DCE=60°∠BCE1=15°,
∴∠D1CB=45°,
∴OC平分∠ACB,
∴CO⊥AB,OA=OB,
∴OC=OA=
AB=
×6=3,
∴OD=CD-OC=7-3=4,
在Rt△AOD1中,AD1=
=
=5.
故答案为5.
∴∠DCE=60°,△ABC为等腰直角三角形,
∵三角板DCE绕着点C顺时针旋转15°得到△D1CE1,
∴∠D1CE1=∠DCE=60°∠BCE1=15°,
∴∠D1CB=45°,
∴OC平分∠ACB,
∴CO⊥AB,OA=OB,
∴OC=OA=
| 1 |
| 2 |
| 1 |
| 2 |
∴OD=CD-OC=7-3=4,
在Rt△AOD1中,AD1=
| AO2+OD12 |
| 32+42 |
故答案为5.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等腰直角三角形的性质和勾股定理.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 如图,CD是⊙O的弦,且CD=6.根据以上条件你能求出⊙O的半径吗?
如图,CD是⊙O的弦,且CD=6.根据以上条件你能求出⊙O的半径吗? 已知:如图,直线AB与直线CD相交于点O,∠AOD与∠BOC是对顶角.求证:∠AOD=∠BOC.
已知:如图,直线AB与直线CD相交于点O,∠AOD与∠BOC是对顶角.求证:∠AOD=∠BOC. 如图,A为反比例函数
如图,A为反比例函数 如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的E处,那么AE为
如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的E处,那么AE为