题目内容
16.一个袋中装有6个红球,5个黄球,3个白球,每个球除颜色外都相同,任意摸出一球,摸到白球的可能性最小.分析 分别求出摸出各种颜色球的概率,即可比较出摸出何种颜色球的可能性最小.
解答 解:因为袋中装有6个红球,5个黄球,3个白球,共有14个球,
①为红球的概率是$\frac{6}{14}$=$\frac{3}{7}$;
②为黄球的概率是$\frac{5}{14}$;
③为白球的概率是$\frac{3}{14}$;
所以摸出白球的可能性最小.
故答案为:白.
点评 本题主要考查可能性的大小,只需求出各自所占的比例大小即可,求比例时,应注意记清各自的数目.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
11.下列单项式中,次数为3的是( )
| A. | x3y | B. | x2y | C. | 3xy | D. | 3y |
5.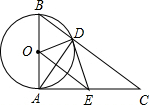 如下图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:
如下图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:
①ED是⊙O的切线;②BC=2OE;③△BOD为等边三角形;④△EOD∽△CAD
正确的是( )
 如下图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:
如下图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:①ED是⊙O的切线;②BC=2OE;③△BOD为等边三角形;④△EOD∽△CAD
正确的是( )
| A. | ①② | B. | ②④ | C. | ①②④ | D. | ①②③④ |
6.$\sqrt{(-4)^{2}}$的平方根是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±4 |
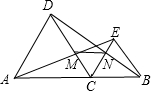 如图,点C是线段AB上的任意一点(C点不与A、B点重合),分别以AC、BC为边在直线AB的同侧作等边三角形△ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N.
如图,点C是线段AB上的任意一点(C点不与A、B点重合),分别以AC、BC为边在直线AB的同侧作等边三角形△ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N. 本商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).
本商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).