题目内容
6.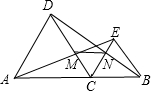 如图,点C是线段AB上的任意一点(C点不与A、B点重合),分别以AC、BC为边在直线AB的同侧作等边三角形△ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N.
如图,点C是线段AB上的任意一点(C点不与A、B点重合),分别以AC、BC为边在直线AB的同侧作等边三角形△ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N.(1)△ACE≌△DCB;
(2)△ACM≌△DCN;
(3)MN∥AB.
分析 (1)由等边三角形的性质得出AC=CD,BC=CE,∠ACD=∠BCE=60°,得出∠DCB=∠ACE,由SAS即可得出△ACE≌△DCB;
(2)由全等三角形的性质得出∠EAC=∠BDC,再证出∠ACD=∠DCE,由ASA证明△ACM≌△DCN即可;
(3)由全等三角形的性质得出CM=CN,证出△MCN是等边三角形,得出∠MNC=∠NCB=60°,即可得出结论.
解答 证明:(1)∵△ACD和△BCE是等边三角形,
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,∠DCB=∠ACE,
在△ACE与△DCB中,
$\left\{\begin{array}{l}{AC=CD}&{\;}\\{∠DCB=∠ACE}&{\;}\\{BC=CE}&{\;}\end{array}\right.$,
∴△ACE≌△DCB(SAS);
(2)由(1)得:△ACE≌△DCB,
∴∠EAC=∠BDC,
∵∠ACD=∠BCE=60°,
∴∠DCE=60°,
∴∠ACD=∠DCE,
在△ACM与△DCN中,
$\left\{\begin{array}{l}{∠EAC=∠BDC}&{\;}\\{AC=DC}&{\;}\\{∠ACD=∠BCE}&{\;}\end{array}\right.$,
∴△ACM≌△DCN(ASA).
(3)由(2)得:△ACM≌△DCN,
∴CM=CN,
又∵∠MCN=180°-60°-60°=60°,
∴△MCN是等边三角形,
∴∠MNC=60°=∠NCB,
∴MN∥AB.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质、平行线的判定;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
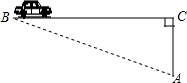 超速行驶是引发交通事故的主要原因之一,上周末,小明和三位同学尝试用自己所学的知识检测车速,如图8,观测点设在A处,离娄新高速的距离(AC)为30m,这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为4s,∠BAC=75°.
超速行驶是引发交通事故的主要原因之一,上周末,小明和三位同学尝试用自己所学的知识检测车速,如图8,观测点设在A处,离娄新高速的距离(AC)为30m,这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为4s,∠BAC=75°.
 如图,在△ABC中,AD是中线,BE交AD于F,且AE=EF,求证:AC=BF.
如图,在△ABC中,AD是中线,BE交AD于F,且AE=EF,求证:AC=BF.
 如图,直线AB和CD交于点O,∠COE=90°,OD平分∠BOF,∠BOE=50°.
如图,直线AB和CD交于点O,∠COE=90°,OD平分∠BOF,∠BOE=50°.