题目内容
6.(1)计算:($\sqrt{3}$-1)2-($\sqrt{2}-\sqrt{3}$)($\sqrt{2}+\sqrt{3}$);(2)已知y=$\sqrt{4x-1}$+$\sqrt{1-4x}$+9,求$\sqrt{36x+y}$的值.
分析 (1)根据完全平方公式和平方差公式计算;
(2)根据二次根式有意义的条件得到4x-1≥0且1-4x≥0,解得x=$\frac{1}{4}$,再计算出对应的y的值,然后把x、y的值代入原式后化简即可.
解答 解:(1)原式=3-2$\sqrt{3}$+1-(2-3)
=4-2$\sqrt{3}$+1
=5-2$\sqrt{3}$;
(2)根据题意得4x-1≥0且1-4x≥0,解得x=$\frac{1}{4}$
所以y=9,
所以原式=$\sqrt{36×\frac{1}{4}+9}$
=$\sqrt{18}$
=3$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了二次根式有意义的条件.

练习册系列答案
相关题目
1.以下说法:
①若直角三角形的两边长为3与4,则第三次边长是5;
②两边及其第三边上的中线对应相等的两个三角形全等;
③长度等于半径的弦所对的圆周角为30°
④反比例函数y=-$\frac{2}{x}$,当>0时y随x的增大而增大,
正确的有( )
①若直角三角形的两边长为3与4,则第三次边长是5;
②两边及其第三边上的中线对应相等的两个三角形全等;
③长度等于半径的弦所对的圆周角为30°
④反比例函数y=-$\frac{2}{x}$,当>0时y随x的增大而增大,
正确的有( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
11.如图,已知等腰直角三角形的腰长为1,按图1的方法剪取一个正方形,成为第一次剪取,记所得正方形面积为s1;按照图1的剪法,在余下的△ADE和△BDF中,分别剪取两个全等的正方形,称为第2次剪取,并记这两个正方形面积之和为s2(如图2);再在余下的四个三角形中,用同样的方法分别剪去正方形,得到四个全等的正方形,成为第3次剪取,并记这四个正方形面积之和为S3(如图3);继续剪取下去…;则第n此剪取时,Sn=( )


| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{2}^{n+1}}$ | D. | 1-$\frac{1}{{2}^{n}}$ |
18.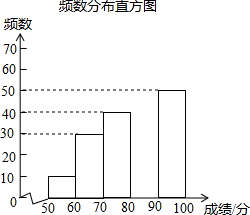 中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校1500名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了部分参赛学生的成绩作为样本进行处理,得到下列不完整的统计图表.请你根据表中提供的信息,解答下列问题:
中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校1500名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了部分参赛学生的成绩作为样本进行处理,得到下列不完整的统计图表.请你根据表中提供的信息,解答下列问题:
(1)此次调查的样本容量为200;
(2)在表中:m=70; n=0.2;
(3)补全频数分布直方图;
(4)若成绩在80分以上(包括80分)的为“优”等,则该校参加这次比赛的1500名学生中,成绩“优”等约有多少人?
 中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校1500名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了部分参赛学生的成绩作为样本进行处理,得到下列不完整的统计图表.请你根据表中提供的信息,解答下列问题:
中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校1500名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了部分参赛学生的成绩作为样本进行处理,得到下列不完整的统计图表.请你根据表中提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
(2)在表中:m=70; n=0.2;
(3)补全频数分布直方图;
(4)若成绩在80分以上(包括80分)的为“优”等,则该校参加这次比赛的1500名学生中,成绩“优”等约有多少人?
16.点B(3,-1)一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图△ABC中,DE垂直平分AC交AB于E,∠A=25°,∠ACB=80°,则∠BCE=55度.
如图△ABC中,DE垂直平分AC交AB于E,∠A=25°,∠ACB=80°,则∠BCE=55度.