题目内容
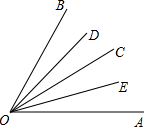 如图,已知∠AOB=60°,OC是∠AOB的平分线,OD、OE分别平分∠BOC和∠AOC.
如图,已知∠AOB=60°,OC是∠AOB的平分线,OD、OE分别平分∠BOC和∠AOC.(1)求∠DOE的度数;
(2)当OC在∠AOB内绕O点旋转时,OD、OE还是∠BOC、∠AOC的平分线?问此时∠DOE的度数是否与(1)中相同?通过此过程,你总结出怎样的结论?
考点:角平分线的定义
专题:
分析:(1)根据角平分线的定义求得∠AOC=∠BOD=
∠AOB,再由角平分线的定义求得,∠DOC=
∠BOC,∠EOC=
∠AOC即可求解;
(2)根据角平分线的定义求得,∠DOE=∠COE+∠DOC=
(∠AOC+∠BOC)=
∠AOB,从而解决问题.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据角平分线的定义求得,∠DOE=∠COE+∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵OC平分∠AOB,∠AOB=60°
∴∠AOC=∠BOC=
∠AOB=
×60°=30°
又∵OD平分∠BOC.OE平分∠AOC
∴∠DOC=
∠BOC=
×30°=15°.∠COE=
∠AOC=
×30°=15°
∴∠DOE=∠COE+∠DOC=15°+15°=30°
(2)相同
理由:∵OE平分∠A OC,
∴∠COE=
∠AOC
∵OD平分∠BOC,
∴∠DOC=
∠BOC
∵∠AOB=40°,
∴∠DOE=∠COE+∠DOC
=
∠AOC+
∠BOC
=
(∠AOC+∠BOC)
=
∠AOB
=
×60°
=30°
结论:∠DOE的大小与射线OC在∠AOB内部的位置无关.∠DOE总等于30°.
∴∠AOC=∠BOC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵OD平分∠BOC.OE平分∠AOC
∴∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=∠COE+∠DOC=15°+15°=30°
(2)相同
理由:∵OE平分∠A OC,
∴∠COE=
| 1 |
| 2 |
∵OD平分∠BOC,
∴∠DOC=
| 1 |
| 2 |
∵∠AOB=40°,
∴∠DOE=∠COE+∠DOC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=30°
结论:∠DOE的大小与射线OC在∠AOB内部的位置无关.∠DOE总等于30°.
点评:本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )
如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )| A、14 | B、18 | C、24 | D、48 |
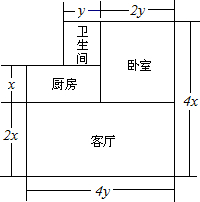 已知房屋的高度为h m,现老板娘在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果某种壁纸的价格是b元/m2,那么购买所需壁纸至少需要多少元?(计算时不扣除门,窗所占的面积)
已知房屋的高度为h m,现老板娘在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果某种壁纸的价格是b元/m2,那么购买所需壁纸至少需要多少元?(计算时不扣除门,窗所占的面积)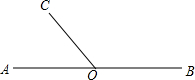 如图,点O为直线AB上一点,∠AOC=50°.
如图,点O为直线AB上一点,∠AOC=50°.