Question

12．成都市某校在推进新课改的过程中，开设的体育选修课有：A-篮球，B-足球，C-排球，D-羽毛球，E-乒乓球，学生可根据自己的爱好选修一门，学校王老师对某班全班同学的选课情况进行调查统计，制成了两幅不完整的统计图（如图）．

（1）求出该班的总人数，并补全频数分布直方图；
（2）求出“足球”在扇形的圆心角是多少度；
（3）该班班委4人中，1人选修篮球，2人选修足球，1人选修排球，李老师要从这4人中人任选2人了解他们对体育选课的看法，请你用列表或画树状图的方法，求选出的2人恰好1人选修篮球，1人选修足球的概率．

Answer 1

分析 （1）由C有12人，占24%，即可求得该班的总人数，继而求得A与E的人数，即可补全频数分布直方图；
（2）由（1）可得“足球”在扇形的圆心角是360°×$\frac{7}{50}$；
（3）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与选出的2人恰好1人选修篮球，1人选修足球的情况，再利用概率公式即可求得答案．

解答 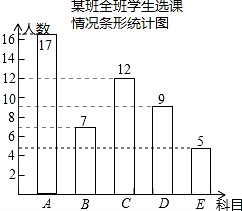解：（1）∵C有12人，占24%，
∴该班的总人数有：12÷24%=50（人），
∴E有：50×10%=5（人），
A有50-7-12-9-5=17（人），
补全频数分布直方图为：

（2）“足球”在扇形的圆心角是：360°×$\frac{7}{50}$=50.4°；

（3）画树状图得：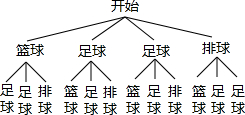

∵共有12种等可能的结果，选出的2人恰好1人选修篮球，1人选修足球的有4种情况，
∴选出的2人恰好1人选修篮球，1人选修足球的概率为：$\frac{4}{12}$=$\frac{1}{3}$．

点评 此题考查的是用列表法或树状图法求概率以及扇形统计图与频数分布直方图的知识．用到的知识点为：概率=所求情况数与总情况数之比．