题目内容
8.先化简,再求值:$\frac{{{x^2}-9}}{x-2}$÷$\frac{{{x^2}-6x+9}}{2x-4}$•$\frac{1}{x+3}$,其中x=5.分析 原式利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{(x+3)(x-3)}{x-2}$•$\frac{2(x-2)}{(x-3)^{2}}$•$\frac{1}{x+3}$=$\frac{2}{x-3}$,
当x=5时,原式=1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3. 如图,△ABC是⊙O的内接三角形,∠A=55°,则∠OCB为( )
如图,△ABC是⊙O的内接三角形,∠A=55°,则∠OCB为( )
 如图,△ABC是⊙O的内接三角形,∠A=55°,则∠OCB为( )
如图,△ABC是⊙O的内接三角形,∠A=55°,则∠OCB为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
13.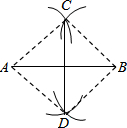 如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
 如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 等腰梯形 |
20.-6的相反数是( )
| A. | 6 | B. | -6 | C. | $\frac{1}{6}$ | D. | $-\frac{1}{6}$ |
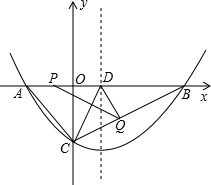 已知抛物线y=ax2+bx+c(a>0)的图象经过点B(12,0)和C(0,-6),对称轴为x=2.
已知抛物线y=ax2+bx+c(a>0)的图象经过点B(12,0)和C(0,-6),对称轴为x=2.



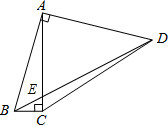 如图,四边形ABCD中,对角线交于点E,∠BAD=∠ACB=90°,AB=AD,若tan∠ABC=4,EC=1,则BE=$\frac{\sqrt{34}}{3}$.
如图,四边形ABCD中,对角线交于点E,∠BAD=∠ACB=90°,AB=AD,若tan∠ABC=4,EC=1,则BE=$\frac{\sqrt{34}}{3}$.