题目内容
18.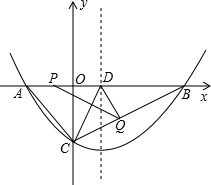 已知抛物线y=ax2+bx+c(a>0)的图象经过点B(12,0)和C(0,-6),对称轴为x=2.
已知抛物线y=ax2+bx+c(a>0)的图象经过点B(12,0)和C(0,-6),对称轴为x=2.(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点Q的运动速度;若不存在,请说明理由;
(3)在(2)的结论下,直线x=1上是否存在点M使,△MPQ为等腰三角形?若存在,请写出所有点M的坐标(请直接写出答案);若不存在,请说明理由.
【提示:抛物线y=ax2+bx+c(a≠0)的对称轴是x=-$\frac{b}{2a}$,顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)】
分析 (1)把B(12,0)和C(0,-6)代入解析式,然后根据对称轴公式得到关于a,b的方程组,解方程组即可求得;
(2)根据勾股定理求得AC=AD=10,然后通过证得DQ∥AC,得出$\frac{BD}{AD}$=$\frac{BQ}{CQ}$,根据DB=AD=10,得出BQ=CQ,根据三角形中位线定理得出DQ=$\frac{1}{2}$AC=5,进而求得AP=AD-PD=AD-DQ=10-5=5,所以存在t=5(秒)时,线段PQ被直线CD垂直平分,根据勾股定理求得CQ=3$\sqrt{5}$,进而就可求得点Q的运动速度;
(3)求得P、Q的坐标,设M(1,y),分三种情况利用勾股定理列出关于y的方程,解方程求得即可.
解答 解:(1)∵抛物线过C(0,-6),
∴c=-6,即y=ax2+bx-6,
则$\left\{\begin{array}{l}{-\frac{b}{2a}=2}\\{144a+12b-6=0}\end{array}\right.$,
解得:a=$\frac{1}{16}$,b=-$\frac{1}{4}$,
∴该抛物线的解析式为y=$\frac{1}{16}$x2-$\frac{1}{4}$x-6;
(2)存在;
设直线CD垂直平分PQ,
∵B(12,0),C(0,-6),对称轴为x=2,
∴A(-8,0),
∴OA=8,OC=6,
在Rt△AOC中,AC=$\sqrt{{8}^{2}+{6}^{2}}$=10=AD,
∴点D在对称轴上,连结DQ 显然∠PDC=∠QDC,
由已知∠PDC=∠ACD,
∴∠QDC=∠ACD,
∴DQ∥AC,
∴$\frac{BD}{AD}$=$\frac{BQ}{CQ}$,
∵AB=20,AD=10,
∴DB=AB-AD=20-10=10=AD,
∴$\frac{BQ}{CQ}$=1,
∴BQ=CQ,
∴DQ为△ABC的中位线,
∴DQ=$\frac{1}{2}$AC=5.
AP=AD-PD=AD-DQ=10-5=5,
∴t=5÷1=5(秒),
∴存在t=5(秒)时,线段PQ被直线CD垂直平分,
在Rt△BOC中,BC=$\sqrt{{6}^{2}+1{2}^{2}}$=6$\sqrt{5}$,
∴CQ=3$\sqrt{5}$,
∴点Q的运动速度为每秒$\frac{3\sqrt{5}}{5}$单位长度.
(3)∵PD=DQ=5,
∴P(-3,0),
∵B(12,0)和C(0,-6),BQ=CQ,
∴Q(6,-3),
设M(1,y),
当PM=QM时,则(-3-1)2+(0-y)2=(6-1)2+(-3-y)2,
解得y=-3,
∴M1(1,-3);
当PQ=PM时,则(-3-1)2+(0-y)2=(-3-6)2+(0+3)2
解得y=±$\sqrt{74}$,
∴M2(1,$\sqrt{74}$),M3(1,-$\sqrt{74}$),
当PQ=QM时,则(6-1)2+(-3-y)2=(-3-6)2+(0+3)2,
解得y=-3±$\sqrt{65}$,
∴M4(1,-3+$\sqrt{65}$),M5((1,-3-$\sqrt{65}$).
综上,存在这样的五点:M1(1,-3),M2(1,$\sqrt{74}$),M3(1,-$\sqrt{74}$),M4(1,-3+$\sqrt{65}$),M5((1,-3-$\sqrt{65}$).
点评 本题是二次函数的综合题,考查了待定系数法求二次函数的解析式,线段的垂直平分线的性质,等腰三角形的性质,平行线的判定和性质,三角形中位线的性质,勾股定理的应用等,熟练掌握性质定理以及求解析式的方法是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 5000(1+x)2=8000 | B. | 5000x2=8000 | ||
| C. | 5000(1+x%)2=8000 | D. | 5000(1+x)+5000(1+x)2=8000 |
| A. | 60° | B. | 45° | C. | 36° | D. | 18° |
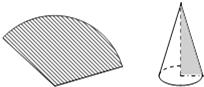 用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )| A. | 2cm | B. | 3$\sqrt{2}$cm | C. | 4$\sqrt{2}$cm | D. | 4cm |
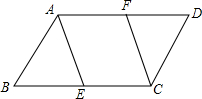 如图,在?ABCD中,点E、F分别是BC、AD的中点
如图,在?ABCD中,点E、F分别是BC、AD的中点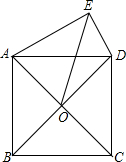 如图,在正方形ABCD中AC与BD交于点O,形外有一点E,使∠AED=90°,且DE=3,OE=4$\sqrt{2}$,则AE=5.
如图,在正方形ABCD中AC与BD交于点O,形外有一点E,使∠AED=90°,且DE=3,OE=4$\sqrt{2}$,则AE=5.