题目内容
3.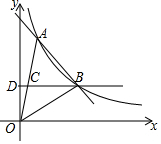 如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
分析 (1)先利用待定系数法求出反比例函数解析式,进而确定出点A的坐标,再用待定系数法求出一次函数解析式;
(2)先求出OB的解析式,进而求出AG,用三角形的面积公式即可得出结论.
解答 解:(1)如图,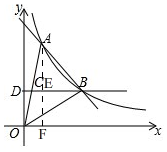 过点A作AF⊥x轴交BD于E,
过点A作AF⊥x轴交BD于E,
∵点B(3,2)在反比例函数y=$\frac{a}{x}$的图象上,
∴a=3×2=6,
∴反比例函数的表达式为y=$\frac{6}{x}$,
∵B(3,2),
∴EF=2,
∵BD⊥y轴,OC=CA,
∴AE=EF=$\frac{1}{2}$AF,
∴AF=4,
∴点A的纵坐标为4,
∵点A在反比例函数y=$\frac{6}{x}$图象上,
∴A($\frac{3}{2}$,4),
∴$\left\{\begin{array}{l}{3k+b=2}\\{\frac{3}{2}k+b=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=6}\end{array}\right.$,
∴一次函数的表达式为y=-$\frac{4}{3}$x+6;
(2)如图1,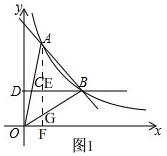 过点A作AF⊥x轴于F交OB于G,
过点A作AF⊥x轴于F交OB于G,
∵B(3,2),
∴直线OB的解析式为y=$\frac{2}{3}$x,
∴G($\frac{3}{2}$,1),
A($\frac{3}{2}$,4),
∴AG=4-1=3,
∴S△AOB=S△AOG+S△ABG=$\frac{1}{2}$×3×3=$\frac{9}{2}$.
点评 此题主要考查了待定系数法,三角形的面积公式,三角形的中位线,解本题的关键是用待定系数法求出直线AB的解析式.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
8.据国家统计局公布,2015年我国国内生产总值约为676700亿元(人民币),用科学记数法表示数据“676700亿”,结果是( )
| A. | 6.767×105 | B. | 6.767×1012 | C. | 6.767×1013 | D. | 6.767×1014 |
15. 如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )
 如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )| A. | 27° | B. | 30° | C. | 36° | D. | 40° |
13.太阳与地球的平均距离大约是150 000 000千米,数据150 000 000用科学记数法表示为( )
| A. | 1.5×108 | B. | 1.5×109 | C. | 0.15×109 | D. | 15×107 |
 如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是( )
如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是( )



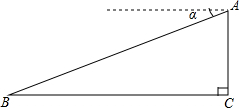 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于4286m(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于4286m(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)