题目内容
15. 如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )| A. | 27° | B. | 30° | C. | 36° | D. | 40° |
分析 由垂径定理得到$\widehat{AC}$=$\widehat{BC}$,根据圆周角定理得到∠AOC=2∠P,由半径OC⊥AB于点D推出△AOD是直角三角形,即可求得∠AOC=54°,即可得到∠P=27°.
解答 解:∵半径OC⊥AB于点D,
∴$\widehat{AC}$=$\widehat{BC}$,
∴∠AOC=2∠P,
∴△AOD是直角三角形,
∴∠AOC=90°-∠A=54°,
∴∠P=27°.
故选A.
点评 本题考查了圆周角定理,垂径定理,熟练掌握定理是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
| A. | y=x2+8x+14 | B. | y=x2-8x+14 | C. | y=x2+4x+3 | D. | y=x2-4x+3 |
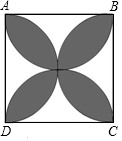 如图,四边形ABCD是边长为1的正方形,用4个半圆覆盖此正方形,得到一个花瓣图案(即阴影部分).
如图,四边形ABCD是边长为1的正方形,用4个半圆覆盖此正方形,得到一个花瓣图案(即阴影部分).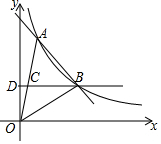 如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.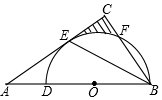 如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. 反比例函数y=$\frac{kb}{x}$的图象如图所示,则一次函数y=kx+b(k≠0)的图象的图象大致是( )
反比例函数y=$\frac{kb}{x}$的图象如图所示,则一次函数y=kx+b(k≠0)的图象的图象大致是( )


