题目内容
11.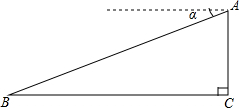 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于4286m(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于4286m(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)
分析 根据直角三角形中正弦函数的定义得sinB=$\frac{AC}{AB}$,即sin16°31′°=$\frac{1200}{AB}$,从而得出答案.
解答 解:在△ABC中,∵∠C=90°,∠B=∠α=43°,AC=1200m,
∴sinB=$\frac{AC}{AB}$,即sin16°31′=$\frac{1200}{AB}$,
∴AB=$\frac{1200}{sin16°31′}$≈$\frac{1200}{0.28}$≈4286(m),
答:飞机A与指挥台B的距离约为4286m.
故答案为4286m.
点评 本题主要考查解直角三角形的应用-仰角俯角问题,熟练掌握仰角俯角的定义和正弦函数的定义是解题的关键.

练习册系列答案
相关题目
2.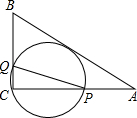 如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( )
如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( )
 如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( )
如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是( )| A. | 4.75 | B. | 4.8 | C. | 5 | D. | 4$\sqrt{2}$ |
16.下列运算正确的是( )
| A. | 5x2•x3=5x5 | B. | 2x+3y=5xy | C. | 4x8÷2x2=4x4 | D. | (-x3)2=x5 |
20.矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
| A. | y=x2+8x+14 | B. | y=x2-8x+14 | C. | y=x2+4x+3 | D. | y=x2-4x+3 |
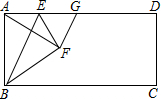 如图,在矩形ABCD中,点E是AD上的一个动点,连结BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设$\frac{AD}{AE}$=n.
如图,在矩形ABCD中,点E是AD上的一个动点,连结BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设$\frac{AD}{AE}$=n.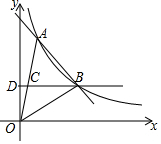 如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.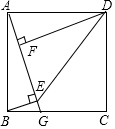 如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.