题目内容
 如图,在△ABC中,已知AB=4,AC=3,BC边上的高AD=2,则△ABC的外接圆半径等于
如图,在△ABC中,已知AB=4,AC=3,BC边上的高AD=2,则△ABC的外接圆半径等于考点:圆周角定理,相似三角形的判定与性质
专题:
分析:根据题意画出图形,连接OA并延长,与圆O交于M,连接BM,由AM为直径,根据直径所对的圆周角为直角,得到∠ABM为90°,又∠M和∠C都为
所对的圆周角,根据同弧所对的圆周角相等可得∠M和∠C相等,进而得到两角的正弦值相等,相似三角形的判定与性质可得出比例式,由已知AB,AC及AD的长即可求出直径AM的长.
 |
| AB |
解答: 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:
连接AO,延长AO交⊙O于点M,连接BM.
∵AD是BC边上的高,
∴△ABD,△ADC都是直角三角形,
又∵AM是直径,则∠ABM=90°,
则∠ABM=∠ADC.
由圆周角定理知,∠C=∠M,
△ACD∽△AMB,
∴
=
,
又∵AC=3,AD=2,AB=4,
∴AM=
=6.
故答案是:6.
 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:连接AO,延长AO交⊙O于点M,连接BM.
∵AD是BC边上的高,
∴△ABD,△ADC都是直角三角形,
又∵AM是直径,则∠ABM=90°,
则∠ABM=∠ADC.
由圆周角定理知,∠C=∠M,
△ACD∽△AMB,
∴
| AD |
| AC |
| AB |
| AM |
又∵AC=3,AD=2,AB=4,
∴AM=
| 3×4 |
| 2 |
故答案是:6.
点评:此题考查了圆周角定理,相似三角形的判定与性质,利用了数形结合的思想,根据题意画出相应的图形,借助图形作出辅助线是解本题的关键.

练习册系列答案
相关题目
 如图中图形,其中的相似图形有
如图中图形,其中的相似图形有 如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m-n-3|+
如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m-n-3|+ 如图,已知,在△ABC中,CD交AB于点E,AE:EB=1:3,EF∥BC∥AD,EF交AC于点F,S△ADE=a.求S△BCE和S△AEF的值.
如图,已知,在△ABC中,CD交AB于点E,AE:EB=1:3,EF∥BC∥AD,EF交AC于点F,S△ADE=a.求S△BCE和S△AEF的值. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E. 已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a-b+c<0.其中正确的结论有( )
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a-b+c<0.其中正确的结论有( ) 用小立方块搭一个几何体,使得从左面和上面看得到的平面图形分别为图所示的图(甲)(乙)这样的几何体最少需要多少个小立方块?最多需要多少个小立方块?你能画出需要最多的从正面看到的图形么?
用小立方块搭一个几何体,使得从左面和上面看得到的平面图形分别为图所示的图(甲)(乙)这样的几何体最少需要多少个小立方块?最多需要多少个小立方块?你能画出需要最多的从正面看到的图形么?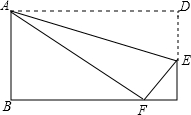 如图,矩形ABCD边上AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,求FE的长.
如图,矩形ABCD边上AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,求FE的长.