题目内容
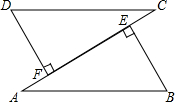如图，AB=CD，DF⊥AC于F，BE⊥AC于E，DF=BE，求证：AF=CE．考点：全等三角形的判定与性质
专题：证明题
分析：利用“HL”证明Rt△ABE和Rt△CDF全等，根据全等三角形对应边相等可得AE=CF，然后求解即可．
解答：证明：∵DF⊥AC，BE⊥AC，
∴∠AEB=∠CFD=90°，
在Rt△ABE和Rt△CDF中，
，
∴Rt△ABE≌Rt△CDF（HL），
∴AE=CF，
∴AE-EF=CF-EF，
即AF=CE．
∴∠AEB=∠CFD=90°，
在Rt△ABE和Rt△CDF中，
|
∴Rt△ABE≌Rt△CDF（HL），
∴AE=CF，
∴AE-EF=CF-EF，
即AF=CE．
点评：本题考查了全等三角形的判定与性质，熟练掌握三角形全等判定方法是解题的关键．
练习册系列答案
相关题目
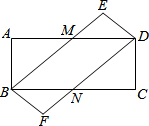如图，在矩形ABCD和矩形BFDE中，AD与BE交于点M，BC与DF交于点N．
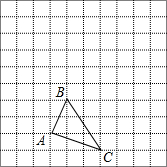如图，已知单位长度为1的方格中有个△ABC．