题目内容
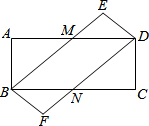 如图,在矩形ABCD和矩形BFDE中,AD与BE交于点M,BC与DF交于点N.
如图,在矩形ABCD和矩形BFDE中,AD与BE交于点M,BC与DF交于点N.(1)四边形BNDM一定是平行四边形吗?为什么?
(2)在什么条件下,四边形BNDM是菱形说明理由.
考点:矩形的性质,平行四边形的判定,菱形的判定
专题:
分析:(1)利用两组对边分别平行的四边形是平行四边形判定四边形BNDM是平行四边形即可;
(2)添加条件AB=BF,运用AAS可证明Rt△ABM≌Rt△FBN,得BM=BN.根据有一邻边相等的平行四边形是菱形得证.
(2)添加条件AB=BF,运用AAS可证明Rt△ABM≌Rt△FBN,得BM=BN.根据有一邻边相等的平行四边形是菱形得证.
解答:证明:(1)∵两个完全相同的矩形纸片ABCD、BFDE,根据矩形的对边平行,
∴BC∥AD,BE∥DF,
∴四边形BNDM是平行四边形,
(2)当AB=BF时,四边形BNDM是菱形.
∵∠ABM+∠MBN=90°,∠MBN+∠FBN=90°,
∴∠ABM=∠FBN.
在△ABM和△FBN中,
,
∴△ABM≌△FBN(ASA),
∴BM=BN,
∴四边形BNDM是菱形.
∴BC∥AD,BE∥DF,
∴四边形BNDM是平行四边形,
(2)当AB=BF时,四边形BNDM是菱形.
∵∠ABM+∠MBN=90°,∠MBN+∠FBN=90°,
∴∠ABM=∠FBN.
在△ABM和△FBN中,
|
∴△ABM≌△FBN(ASA),
∴BM=BN,
∴四边形BNDM是菱形.
点评:本题考查了菱形的判定及矩形的性质,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定.

练习册系列答案
相关题目
 如图,在反比例函数y=
如图,在反比例函数y=| k |
| x |
| A、S1>S2>S3 |
| B、S1<S2<S3 |
| C、S1<S3<S2 |
| D、S1=S2=S3 |
将二次函数的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是y=x2,则原二次函数图象的函数表达式是( )
| A、y=(x-1)2+2 |
| B、y=(x+1)2+2 |
| C、y=(x-1)2-2 |
| D、y=(x+1)2-2 |
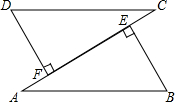 如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE,求证:AF=CE.
如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE,求证:AF=CE.