题目内容
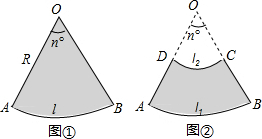
5.如图①,半径为R,圆心角为n°的扇形面积是S扇形=$\frac{nπ{R}^{2}}{360}$,由弧长l=$\frac{nπR}{180}$,得S扇形=$\frac{nπ{R}^{2}}{360}$=$\frac{1}{2}$•$\frac{nπR}{180}$•R=$\frac{1}{2}$lR.通过观察,我们发现S扇形=$\frac{1}{2}$lR类似于S三角形=$\frac{1}{2}$×底×高.类比扇形,我们探索扇环(如图②,两个同心圆围成的圆环被扇形截得的一部分叫做扇环)的面积公式及其应用.
(1)设扇环的面积为S扇环,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形=$\frac{1}{2}$×(上底+下底)×高,用含l1,l2,h的代数式表示S扇环,并证明;
(2)用一段长为40m的篱笆围成一个如图②所示的扇环形花园,线段AD的长h为多少时,花园的面积最大,最大面积是多少?
分析 (1)根据扇形公式之间的关系,结合已知条件推出结果即可;
(2)求出l1+l2=40-2h,代入(1)的结果,化成顶点式,即可得出答案.
解答 (1)S扇环=$\frac{1}{2}$(l1+l2)h,
证明:设大扇形半径为R,小扇形半径为r,圆心角度数为n,则由l=$\frac{nπr}{180}$,得R=$\frac{180{l}_{1}}{nπ}$,r=$\frac{180{l}_{2}}{nπ}$
所以图中扇环的面积S=$\frac{1}{2}$×l1×R-$\frac{1}{2}$×l2×r
=$\frac{1}{2}$l1•$\frac{180{l}_{1}}{nπ}$-$\frac{1}{2}$l2•$\frac{180{l}_{2}}{nπ}$
=$\frac{90}{nπ}$(l12-l22)
=$\frac{90}{nπ}$(l1+l2)(l1-l2)
=$\frac{1}{2}$•$\frac{180}{nπ}$•($\frac{nπ}{180}$R+$\frac{nπ}{180}$r)(l1-l2)
=$\frac{1}{2}$(l1+l2)(R-r)
=$\frac{1}{2}$(l1+l2)h,
故猜想正确.
(2)解:根据题意得:l1+l2=40-2h,
则S扇环=$\frac{1}{2}$(l1+l2)h
=$\frac{1}{2}$(40-2h)h
=-h2+20h
=-(h-10)2+100
∵-1<0,
∴开口向下,有最大值,
当h=10时,最大值是100,
即线段AD的长h为10m时,花园的面积最大,最大面积是100m2.
点评 本题主要考查了扇形面积公式,弧长公式,二次函数的顶点式的应用,能猜想出正确结论是解此题的关键,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知a是整数,则在①$\frac{3a+2}{5}$,②$\frac{6a-5}{7}$,③$\frac{3a+1}{6}$,④$\frac{13a-60}{17}$这四个式子中,可能得整数值的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80cm,则这块扇形铁皮的半径是( )
| A. | 24cm | B. | 48cm | C. | 96cm | D. | 192cm |
14.二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1),则a+b+1的值是( )
| A. | -3 | B. | -1 | C. | 2 | D. | 3 |
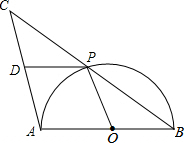 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.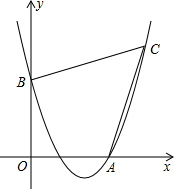 如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).