题目内容
4.若a+b+c=0,且abc≠0,则a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{a}$+$\frac{1}{c}$)+c($\frac{1}{a}$+$\frac{1}{b}$)的值为( )| A. | 1 | B. | 0 | C. | -1 | D. | -3 |
分析 由已知得:a+b=-c,b+c=-a,a+c=-b,再将所求的式子去括号后,同分母加在一起,分别将所求的式子整体代入约分即可.
解答 解:∵a+b+c=0,
∴a+b=-c,b+c=-a,a+c=-b,
a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{a}$+$\frac{1}{c}$)+c($\frac{1}{a}$+$\frac{1}{b}$),
=$\frac{a}{b}$+$\frac{a}{c}$+$\frac{b}{a}$+$\frac{b}{c}$+$\frac{c}{a}$+$\frac{c}{b}$,
=$\frac{a+c}{b}$+$\frac{b+c}{a}$+$\frac{a+b}{c}$,
=$\frac{-b}{b}$+$\frac{-a}{a}$+$\frac{-c}{c}$,
=-1-1-1,
=-3,
故选D.
点评 本题主要考查整式的加减运算和分式的混合运算,熟练掌握整式的运算和分式的混合运算的顺序和法则是解题的关键.

练习册系列答案
相关题目
12. 如图所示,以BC为边的三角形共有( )
如图所示,以BC为边的三角形共有( )
 如图所示,以BC为边的三角形共有( )
如图所示,以BC为边的三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.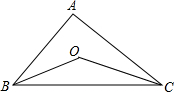 如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
 如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )
如图所示,△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=100°,则∠BOC的度数为( )| A. | 140° | B. | 120° | C. | 90° | D. | 80° |
9. 用一副三角板拼出如图所示的图形,则图中∠α的度数为( )
用一副三角板拼出如图所示的图形,则图中∠α的度数为( )
 用一副三角板拼出如图所示的图形,则图中∠α的度数为( )
用一副三角板拼出如图所示的图形,则图中∠α的度数为( )| A. | 120° | B. | 105° | C. | 100° | D. | 95° |
16. 在下列有理数运算中,不能借助下面数轴解释的是( )
在下列有理数运算中,不能借助下面数轴解释的是( )
 在下列有理数运算中,不能借助下面数轴解释的是( )
在下列有理数运算中,不能借助下面数轴解释的是( )| A. | (-3)+(-3)=-6 | B. | (-3)×2=-6 | C. | 2×(-3)=-6 | D. | 3×(-2)=-6 |
13.下列说法中,正确的是( )
| A. | 0是单项式 | B. | 单项式x2y的次数是2 | ||
| C. | 多项式ab+3是一次二项式 | D. | 单项式-$\frac{1}{3}$πx2y的系数是-$\frac{1}{3}$ |
14.为了了解某班学生每天使用零花钱的情况,随机调查了15名同学,结果如下,下列说法正确的是( )
| 每天零花钱(元) | 0 | 5 | 10 | 15 | 20 |
| 人数 | 2 | 3 | 2 | 6 | 2 |
| A. | 众数是20元 | B. | 平均数是11元 | C. | 极差是15元 | D. | 中位数是10元 |