题目内容
9.已知一直角三角形的木板,三边的平方和为1800,则斜边长为( )| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
分析 设出直角三角形的两直角边分别为a,b,斜边为c,利用勾股定理列出关系式,再由三边的平方和为1800,列出关系式,联立两关系式,即可求出斜边的长.
解答 解:设直角三角形的两直角边分别为a,b,斜边为c,
根据勾股定理得:a2+b2=c2,
∵a2+b2+c2=1800,
∴2c2=1800,即c2=900,
则c=30;
故选:C.
点评 此题考查了勾股定理的应用,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
11.在△ABC中,∠A=30°,∠B=50°,则∠C为( )
| A. | 30° | B. | 50° | C. | 80° | D. | 100° |
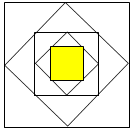 如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)
如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)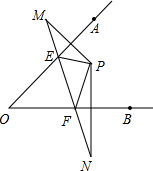 如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是30cm,则线段MN的长是30cm.
如图,点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F,若△PEF的周长是30cm,则线段MN的长是30cm.