题目内容
17.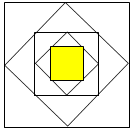 如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)
如图,把一个正方形各边中点连结起来组成第二个正方形,再把第二个正方形各边的中点连结起来组成第三个正方形,按照这样的方法连结得到的第五个正方形的面积占第一个正方形面积的$\frac{1}{16}$.(填几分之几)
分析 先根据正方形的边长是1,得出斜边的长,根据面积公式计算出第二个正方形的面积,以此类推,得出第三个正方形的面积,总结出规律,得到第n个正方形的面积,再把n=5时代入即可求出答案.
解答 解:∵正方形的边长是1,
所以它的斜边长是:$\sqrt{({\frac{1}{2})}^{2}+(\frac{1}{2})^{2}}$=$\sqrt{\frac{1}{2}}$,
所以第二个正方形的面积是:$\sqrt{\frac{1}{2}}$×$\sqrt{\frac{1}{2}}$=$\frac{1}{2}$,
第三个正方形的面积为$\frac{1}{4}$=($\frac{1}{2}$)2,
以此类推,第n个正方形的面积为($\frac{1}{2}$)n-1,
所以第五个正方形的面积是($\frac{1}{2}$)5-1=$\frac{1}{16}$;
故答案为$\frac{1}{16}$.
点评 本题考查了正方形的性质以及图形的变化类,解题的关键是掌握中位线定理和正方形的性质,计算出各边的长,再根据面积公式求出答案.

练习册系列答案
相关题目
9.已知一直角三角形的木板,三边的平方和为1800,则斜边长为( )
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
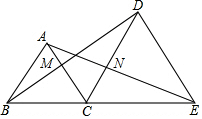 如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,BD与AC交于点M,AE与CD交于点N.
如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,BD与AC交于点M,AE与CD交于点N.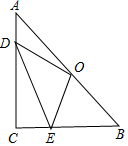 在Rt△ABC中,点O为斜边AB的中点,D、E分别在边AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,则OD+DE+EO的最小值为10.
在Rt△ABC中,点O为斜边AB的中点,D、E分别在边AC、BC上,若CB=6,CA=8,高CH=$\frac{24}{5}$,则OD+DE+EO的最小值为10.