题目内容
 如图,点P、Q分别为矩形ABCD中AB、BC上两点,AB=18cm、AD=4cm,AP=2x,BQ=x,设△PBQ的面积为y(cm2).
如图,点P、Q分别为矩形ABCD中AB、BC上两点,AB=18cm、AD=4cm,AP=2x,BQ=x,设△PBQ的面积为y(cm2).(1)求y关于x的函数关系式;
(2)求△PBQ的面积取值范围.
考点:二次函数的应用
专题:几何图形问题
分析:(1)分别表示出PB、BQ的长,然后根据三角形的面积公式列式整理即可得解;
(2)把函数关系式整理成顶点式解析式,然后根据二次函数的最值,从而确定三角形的面积的最值.
(2)把函数关系式整理成顶点式解析式,然后根据二次函数的最值,从而确定三角形的面积的最值.
解答:解:(1)∵S△PBQ=
PB•BQ,PB=AB-AP=18-2x,BQ=x,
∴y=
(18-2x)x,
即y=-x2+9x(0<x≤4);
(2)由(1)知:y=-x2+9x,
∴y=-(x-
)2+
,
∵当0<x≤
时,y随x的增大而增大,
而0<x≤4,
∴当x=4时,y最大值=20,
即△PBQ的取值范围0<x≤20.
| 1 |
| 2 |
∴y=
| 1 |
| 2 |
即y=-x2+9x(0<x≤4);
(2)由(1)知:y=-x2+9x,
∴y=-(x-
| 9 |
| 2 |
| 81 |
| 4 |
∵当0<x≤
| 9 |
| 2 |
而0<x≤4,
∴当x=4时,y最大值=20,
即△PBQ的取值范围0<x≤20.
点评:本题考查了矩形的性质及二次函数的应用,二次函数的最值问题,根据题意表示出PB、BQ的长度是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )
如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
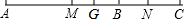 如图,G是AC的中点,M是AB的中点,N是BC的中点,那么下列四个等式中,不成立的是( )
如图,G是AC的中点,M是AB的中点,N是BC的中点,那么下列四个等式中,不成立的是( )| A、MN=GC | ||
B、MG=
| ||
C、GN=
| ||
D、MN=
|
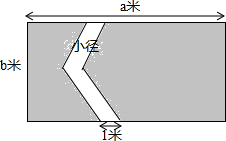 如图,某公园中有一块长a米,宽b米的长方形草坪,为方便游客穿行同时也避免草坪被随意践踏,草坪上用石子铺设了一条宽度均为1米的小径,求铺设小径后草坪(阴影部分)的面积.
如图,某公园中有一块长a米,宽b米的长方形草坪,为方便游客穿行同时也避免草坪被随意践踏,草坪上用石子铺设了一条宽度均为1米的小径,求铺设小径后草坪(阴影部分)的面积. 阅读理解并填空:
阅读理解并填空: 如图,△ABC绕点
如图,△ABC绕点