题目内容
14.在四边形ABCD中,AC⊥BD,点E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH是( )| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 无法确定 |
分析 首先利用三角形的中位线定理证得四边形EFGH为平行四边形,然后利用有一个角是直角的平行四边形是矩形判定即可.
解答  证明:∵点E、F、G、H分别是边AB、BC、CD、DA的中点,
证明:∵点E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=$\frac{1}{2}$AC,GH=$\frac{1}{2}$AC,
∴EF=GH,同理EH=FG
∴四边形EFGH是平行四边形;
又∵对角线AC、BD互相垂直,
∴EF与FG垂直.
∴四边形EFGH是矩形.
故选:A.
点评 本题考查了中点四边形的知识,解题的关键是灵活运用三角形的中位线定理,平行四边形的判断及矩形的判断进行证明,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列各数中,( )是不等式x+3>6的解.
| A. | -4 | B. | 0 | ||
| C. | 4.8 | D. | 以上答案均不正确 |
4.某销售商计划购进甲乙甲乙两种型号的电器共100台,进价与售价情况如下表所示:
(1)求所获总利润y(元)与购进甲型电器x(台)的函数解析式(不写自变量的取值范围).
(2)若所获利润不低于5.5万元,你认为至少要购进多少台乙型电器?
(1)求所获总利润y(元)与购进甲型电器x(台)的函数解析式(不写自变量的取值范围).
(2)若所获利润不低于5.5万元,你认为至少要购进多少台乙型电器?
| 电器类型 | 进价(元)/台 | 售价(元)/台 |
| 甲 | 1500 | 1900 |
| 乙 | 1800 | 2400 |
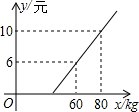 某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要买行李票,已知行李票费y(元)是其重量x(千克)的一次函数,(如图所示):
某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要买行李票,已知行李票费y(元)是其重量x(千克)的一次函数,(如图所示):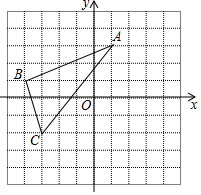 如图,△ABC在平面直角坐标系中,且A(1,3)、B(-4,1)、C(-3,-2).
如图,△ABC在平面直角坐标系中,且A(1,3)、B(-4,1)、C(-3,-2).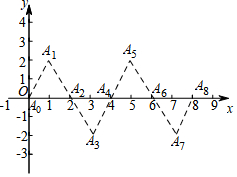 如图所示点A0(0,0),A1(1,2),A2(2,0),A3(3,-2),A4(4,0),…根据这个规律,探究可得点A2017坐标是(2017,2).
如图所示点A0(0,0),A1(1,2),A2(2,0),A3(3,-2),A4(4,0),…根据这个规律,探究可得点A2017坐标是(2017,2).