题目内容
9. 如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=
如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=15°,则∠COE=45°.
分析 根据矩形的性质得出∠ABC=∠BAD=90°,OB=OD,OA=OC,AC=BD,求出OB=OC,OB=OA,根据矩形性质和已知求出∠BAE=∠DAE=45°,求出∠OBC=∠OCB=30°,求出△AOB是等边三角形,推出AB=OB=BE,求出∠OEB=75°,即可求出答案.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=∠BAD=90°,OB=OD,OA=OC,AC=BD,
∴OB=OC,OB=OA,
∴∠OCB=∠OBC,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=180°-90°-45°=45°,
∵∠EAC=15°,
∴∠OCB=∠AEB-∠EAC=45°-15°=30°,
∴∠OBC=∠OCB=30°,
∴∠AOB=30°+30°=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OB,
∵∠BAE=∠AEB=45°,
∴AB=BE,
∴OB=BE,
∴∠OEB=∠EOB,
∵∠OBE=30°,∠OBE+∠OEB+∠BEO=180°,
∴∠OEB=75°,
∵∠OCB=30°,
∴∠COE=∠OEB-∠OCB=45°,
故答案为:45°.
点评 本题考查了矩形的性质,等边三角形的性质和判定,等腰三角形的性质,三角形内角和定理,三角形的外角性质的应用,能求出∠OEB和∠OCB的度数是解此题的关键,综合性比较强,有一定的难度.

练习册系列答案
相关题目
19.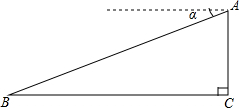 在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )
在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )
 在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )
在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )| A. | 3120米 | B. | 2800$\sqrt{3}$米 | C. | 3260米 | D. | 3000$\sqrt{3}$米 |
20.数轴上A、B两点表示的数分别为-1和$\sqrt{2}$,数轴上点C在点A的左侧,到A点的距离等于点B到点A的距离,则点C所表示的数为( )
| A. | $-2+\sqrt{2}$ | B. | $-1+\sqrt{2}$ | C. | $3-\sqrt{2}$ | D. | $-2-\sqrt{2}$ |
4.下列各条中能确定四边形ABCD是平行四边形的是( )
| A. | AB=CD,AD=BC | B. | ∠A=∠B,∠C=∠D | C. | AB=AD,BC=CD | D. | AB∥CD,AD=BC |
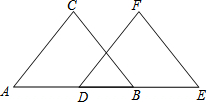 已知:如图,BC∥EF,AD=BE,BC=EF
已知:如图,BC∥EF,AD=BE,BC=EF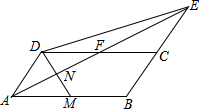 如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E、与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE
如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E、与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE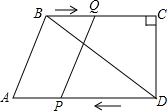 如图,在四边形ABCD中,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,同时动点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,当点P运动到与点A重合时,点Q随之停止.设运动时间为t(秒).
如图,在四边形ABCD中,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,同时动点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,当点P运动到与点A重合时,点Q随之停止.设运动时间为t(秒).