题目内容
14.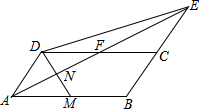 如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E、与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE
如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E、与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE(1)求证:BC=CE;
(2)若DM=2,求DE的长.
分析 (1)利用平行四边形ABCD得出AD=BC,AD∥BC,进一步证得△ADF≌△ECF,得出AD=CE,证得结论;
(2)连接FM、BF,证得四边形AMFD是菱形,得出AN=NF,求得M是AB的中点,利用勾股定理求得AN,进一步得出NE,进一步利用勾股定理求得DE的长即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠FEC,∠ADF=∠ECF,
∵点F为边DC的中点,
∴DF=CF,
在△ADF和△ECF中,
$\left\{\begin{array}{l}{∠DAF=∠FEC}\\{∠ADF=∠ECF}\\{DF=CF}\end{array}\right.$
∴△ADF≌△ECF(AAS),
∴AD=CE,
∴BC=CE.
(2)解:如图,连接FM,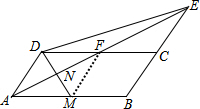
∵DM平分∠ADF,AF平分∠DAB,AB∥DC,AD∥BC,
∴∠DAF=∠BAF=DFN,∠ADM=∠FDM=∠AMD,
∴AD=DF=AM,
∴四边形AMFD是菱形,
∴AF⊥DM,DN=MN=$\frac{1}{2}$DM=1,
又∵DF=FC,DC=AB=6,
∴AM=3,
∴AN=$\sqrt{A{M}^{2}-M{N}^{2}}$=2$\sqrt{2}$,
∴AF=2AN=4$\sqrt{2}$,
∵AF=EF,
∴NE=AE-AN=6$\sqrt{2}$,
∴DE=$\sqrt{N{E}^{2}+D{N}^{2}}$=$\sqrt{73}$.
点评 此题考查平行四边形的性质,三角形全等的判定与性质,菱形判定与性质,勾股定理的运用,正确分析条件与所求问题之间的联系,理清思路解决问题.

练习册系列答案
相关题目
2.以下列各组数为边长,能构成直角三角形的是( )
| A. | 3,3,7 | B. | 3,5,8 | C. | 1.5,2,3 | D. | 6,8,10 |
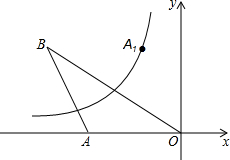 如图,在直角坐标系中,点A的坐标为(-10,0),点B在第二象限,AO=AB,OB=8$\sqrt{5}$,点A关于直线OB的对称点为A1,反比例函数y=$\frac{k}{x}$(k≠0,x<0)的图象经过点A1,则k=-48.
如图,在直角坐标系中,点A的坐标为(-10,0),点B在第二象限,AO=AB,OB=8$\sqrt{5}$,点A关于直线OB的对称点为A1,反比例函数y=$\frac{k}{x}$(k≠0,x<0)的图象经过点A1,则k=-48. 如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=
如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC= 如图所示,将长方形纸条的一角沿虚线CD折叠,DE平分∠BDF,则∠CDE=90°.
如图所示,将长方形纸条的一角沿虚线CD折叠,DE平分∠BDF,则∠CDE=90°.