题目内容
8.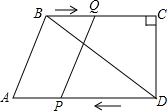 如图,在四边形ABCD中,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,同时动点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,当点P运动到与点A重合时,点Q随之停止.设运动时间为t(秒).
如图,在四边形ABCD中,AD∥BC,∠DCB=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,同时动点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,当点P运动到与点A重合时,点Q随之停止.设运动时间为t(秒).(1)当t为何值时,四边形ABQP是平行四边形?
(2)记PQ与DB的交点为M,问:在点P整个运动过程中,点M的位置是否会发生改变?请说明理由.
(3)是否存在某一时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.
分析 (1)当AP=BQ时,四边形ABQP是平行四边形,据此即可列方程求得;
(2)首先证明△QBM∽△PMD,利用相似三角形的对应边的比相等,求得BD和BM的长,即可求解;
(3)证明△QBM∽△DBC,利用相似三角形的对应边的比相等求得.
解答 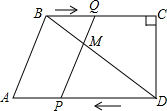 解:(1)依题意得:t=21-2t,
解:(1)依题意得:t=21-2t,
解得:t=7.
答:当t=7时,四边形ABQP是平行四边形;
(2)如图,∵BQ∥PD
∴∠QBM=∠PDM,
又∵∠QMB=∠PMD,
∴△QBM∽△PMD,
∴$\frac{BM}{MD}=\frac{BQ}{PD}$.
又∵BQ=t,PD=2t
∴$\frac{BM}{MD}=\frac{1}{2}$.
在Rt△BDC中,BC=16,DC=12,
∴BD=20,
∴BM=$\frac{20}{3}$(定值)
∴在点P整个运动过程中,点M的位置不会发生改变.
(3)∵PQ⊥BD∠DCB=90°
∴∠BMQ=∠C,
又∵∠MBQ=∠CBD,
∴△QBM∽△DBC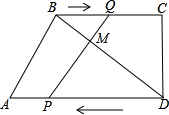 .
.
∴$\frac{BQ}{BD}=\frac{BM}{BC}$
由(2)可知,
∴BM=$\frac{20}{3}$,
∴$\frac{t}{20}=\frac{{\frac{20}{3}}}{16}$,
解得:t=$\frac{5}{6}$.
答:当t=$\frac{5}{6}$时,使得PQ⊥BD.
点评 本题考查平行四边形的判定与相似三角形的判定与性质,理解△QBM∽△PMD,△QBM∽△DBC是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=
如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=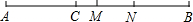 如图,线段AB的长为8cm,C是线段AB上的一点,AC=3.2cm,M是AB的中点,N是CB的中点.
如图,线段AB的长为8cm,C是线段AB上的一点,AC=3.2cm,M是AB的中点,N是CB的中点. 如图,AC和BD相交于点O,且AB∥DC,OC=OD.求证:△OAB是等腰三角形.
如图,AC和BD相交于点O,且AB∥DC,OC=OD.求证:△OAB是等腰三角形. 如图所示,将长方形纸条的一角沿虚线CD折叠,DE平分∠BDF,则∠CDE=90°.
如图所示,将长方形纸条的一角沿虚线CD折叠,DE平分∠BDF,则∠CDE=90°. 如图,将图案绕点O按逆时针方向旋转90°,得到的图案是( )
如图,将图案绕点O按逆时针方向旋转90°,得到的图案是( )


