题目内容
1.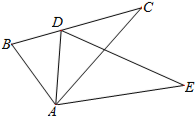 如图,在△ABC中,D是BC上一点,AB=AD,E是△ABC外一点,∠B=∠ADE,∠BAD=∠CAE.
如图,在△ABC中,D是BC上一点,AB=AD,E是△ABC外一点,∠B=∠ADE,∠BAD=∠CAE.(1)求证:AC=AE;
(2)若∠BAD=30°,AB=6,BD=4,DE=9,求△ADC 的面积.
分析 (1)由∠BAD=∠CAE,得出∠BAC=∠DAE,由ASA证得△ABC≌△ADE,即可得出结论;
(2)过点A作AG垂直于BD于G,由AB=AD,得出BG=DG=2,求得AG=$\sqrt{A{B}^{2}-B{G}^{2}}$,再根据△ABC≌△ADE,得出DE=BC=9,求出DC,由S△ADC=$\frac{1}{2}$DC•AG即可得出结果.
解答 (1)证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,$\left\{\begin{array}{l}{∠BAC=∠DAE}\\{AB=AD}\\{∠B=∠ADE}\end{array}\right.$,
∴△ABC≌△ADE(ASA),
∴AC=AE;
(2)解:过点A作AG垂直于BD于G,如图所示: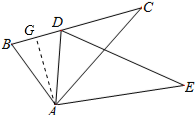 ∵AB=AD,
∵AB=AD,
∴BG=DG=2,
AG=$\sqrt{A{B}^{2}-B{G}^{2}}$=$\sqrt{{6}^{2}-{2}^{2}}$=$4\sqrt{2}$,
∵△ABC≌△ADE,
∴DE=BC=9,
∴DC=BC-BD=9-4=5,
∴S△ADC=$\frac{1}{2}$DC•AG=$\frac{1}{2}$×5×$4\sqrt{2}$=$10\sqrt{2}$.
点评 本题考查了全等三角形的判定与性质、等腰三角形的性质、勾股定理、三角形面积的计算等知识;本题综合性强,难度不大,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
16.分式$\frac{1}{x+1}$有意义的条件是( )
| A. | x≠-1 | B. | x≠0 | C. | x≠1 | D. | x为任意实数 |
6.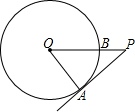 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )
 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{3}$ |
 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,AC⊥x轴于点C,OC=3,连接BC.
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,AC⊥x轴于点C,OC=3,连接BC. 如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=150°.
如图,直线AB、CD相交于点O,∠COE为直角,∠AOE=60°,则∠BOD=150°. 如图,把弯曲的河道改直,能够缩短航程,理由是两点之间线段最短.
如图,把弯曲的河道改直,能够缩短航程,理由是两点之间线段最短.