题目内容
9.甲队原有工人65人,乙队原有工人40人,现又有30名工人调入这两队,为了使乙队人数是甲队人数的$\frac{1}{2}$,应调往甲、乙两队各多少人?分析 设调往甲队x人,调往乙队(30-x)人,则现在甲队人数为(65+x)人,现在乙队人数为(40+30-x)人,利用乙队人数是甲队人数的$\frac{1}{2}$列方程,然后解方程求出x,则计算30-x即可.
解答 解:设调往甲队x人,调往乙队(30-x)人,
根据题意得40+30-x=$\frac{1}{2}$(65+x),
解得:x=25,
所以30-x=30-25=5
答:应调往甲队25人,调往乙队5人.
点评 本题考查了一元一次方程的应用:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.列一元一次方程解应用题的五个步骤.解决本题的关键是表示出调入后甲乙两队的人数.

练习册系列答案
相关题目
18.下列真命题中,逆命题也是真命题的是( )
| A. | 全等三角形的对应角都相等 | |
| B. | 如果两个实数相等,那么这两个实数的平方相等 | |
| C. | 对顶角相等 | |
| D. | 等边三角形每一个都等于60° |
19. 已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),下列结论中错误的是( )
已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),下列结论中错误的是( )
 已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),下列结论中错误的是( )
已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),下列结论中错误的是( )| A. | b2>4ac | |
| B. | 若点(-2,m),(-5,n)在抛物线上,则m>n | |
| C. | ax2+bx+c≥-6 | |
| D. | 关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1 |
 解答题唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
解答题唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
 如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)
如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)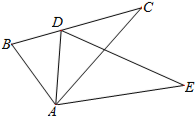 如图,在△ABC中,D是BC上一点,AB=AD,E是△ABC外一点,∠B=∠ADE,∠BAD=∠CAE.
如图,在△ABC中,D是BC上一点,AB=AD,E是△ABC外一点,∠B=∠ADE,∠BAD=∠CAE.