题目内容
6.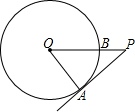 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{3}$ |
分析 根据切线的性质,△OAP是直角三角形,根据勾股定理就可以求出OP=5,则可以求得cos∠APO的值.
解答 解:∵PA为⊙O的切线,A为切点,
∴OA⊥AP.
又∵PA=4,OA=3,∴OP=5.
∴cos∠APO=$\frac{4}{5}$.
故选B.
点评 本题运用了切线的性质定理,通过切线的性质定理得到△OAP是直角三角形,是解决本题的关键.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
16.记max{x,y}表示x,y两个数中的最大值,例如max{1,2}=2,max{7,7}=7,则关于x的一次函数y=max{2x,x+1}可以表示为( )
| A. | y=2x | B. | y=x+1 | C. | y=$\left\{\begin{array}{l}2x(x<1)\\ x+1(x≥1)\end{array}$ | D. | y=$\left\{\begin{array}{l}2x(x>1)\\ x+1(x≤1)\end{array}$ |
18.下列真命题中,逆命题也是真命题的是( )
| A. | 全等三角形的对应角都相等 | |
| B. | 如果两个实数相等,那么这两个实数的平方相等 | |
| C. | 对顶角相等 | |
| D. | 等边三角形每一个都等于60° |
15.3°=( )
| A. | 180′ | B. | 18′ | C. | 30′ | D. | 3′ |
 如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)
如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)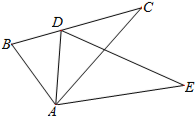 如图,在△ABC中,D是BC上一点,AB=AD,E是△ABC外一点,∠B=∠ADE,∠BAD=∠CAE.
如图,在△ABC中,D是BC上一点,AB=AD,E是△ABC外一点,∠B=∠ADE,∠BAD=∠CAE.