题目内容
抛物线y=
x2+
x-3与y轴交于点C,与x轴交于A、B两点,A点在左边,若点E在x轴上,点P在抛物线上,是否存在以A、C、F、P为顶点,且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
| 3 |
| 4 |
| 9 |
| 4 |
考点:二次函数综合题
专题:
分析:本题应分情况讨论:
①过C作x轴的平行线,与抛物线的交点符合P点的要求,此时P、C的纵坐标相同,代入抛物线的解析式中即可求出P点坐标;
②将AC平移,令C点落在x轴(即E点)、A点落在抛物线(即P点)上;可根据平行四边形的性质,得出P点纵坐标(P、C纵坐标的绝对值相等),代入抛物线的解析式中即可求得P点坐标.
①过C作x轴的平行线,与抛物线的交点符合P点的要求,此时P、C的纵坐标相同,代入抛物线的解析式中即可求出P点坐标;
②将AC平移,令C点落在x轴(即E点)、A点落在抛物线(即P点)上;可根据平行四边形的性质,得出P点纵坐标(P、C纵坐标的绝对值相等),代入抛物线的解析式中即可求得P点坐标.
解答:解:如图所示,
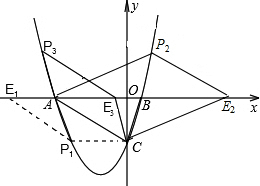
①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,
 ∵C(0,-3)
∵C(0,-3)
∴设P1(x,-3)
∴
x2+
x-3=0,
解得x1=0,x2=-3
∴P1(-3,-3);
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
∵C(0,-3)
∴设P(x,3),
∴
x2+
x-3=3,
x2+3x-8=0
解得x=
或x=
,
此时存在点P2(
,3)和P3(
,3),
综上所述存在3个点符合题意,坐标分别是P1(-3,-3),P2(
,3)和P3(
,3).
①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形,
 ∵C(0,-3)
∵C(0,-3)∴设P1(x,-3)
∴
| 3 |
| 4 |
| 9 |
| 4 |
解得x1=0,x2=-3
∴P1(-3,-3);
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
∵C(0,-3)
∴设P(x,3),
∴
| 3 |
| 4 |
| 9 |
| 4 |
x2+3x-8=0
解得x=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
此时存在点P2(
-3+
| ||
| 2 |
-3-
| ||
| 2 |
综上所述存在3个点符合题意,坐标分别是P1(-3,-3),P2(
-3+
| ||
| 2 |
-3-
| ||
| 2 |
点评:此题考查了二次函数解析式的确定、图形面积的求法、平行四边形的判定和性质、二次函数的应用等知识,综合性强,难度较大.

练习册系列答案
相关题目
 如图,点F是平行四边形ABCD的边CD上一点,直线BF交AD的延长线于点E,已知DE=3,EF=4,FB=3,则BC=
如图,点F是平行四边形ABCD的边CD上一点,直线BF交AD的延长线于点E,已知DE=3,EF=4,FB=3,则BC= 如图,已知△ACE∽△BDE,AC=6,BD=3,AB=12,CD=18.求AE和DE的长.
如图,已知△ACE∽△BDE,AC=6,BD=3,AB=12,CD=18.求AE和DE的长.