题目内容
在直角三角形ABC中,∠C=90°,AD平分∠BAC,A=10,BD=4,求∠A的正切值.
考点:解直角三角形
专题:计算题
分析:作CE⊥AB于E,如图,根据角平分线的性质的DE=DC,设CD=x,AC=y,则DE=x,再证明Rt△ACD≌Rt△AED得AC=AE=y,则BE=AB-AE=10-y,然后证明Rt△BDE∽Rt△BAC,利用相似比得到x=
y;接着在Rt△BDE中,根据勾股定理得x2+(10-y)2=42,则(
y)2+(10-y)2=42,解方程得解得y1=
,y2=10(舍去),则x=
,最后根据正切的定义求解.
| 2 |
| 5 |
| 2 |
| 5 |
| 210 |
| 29 |
| 84 |
| 29 |
解答:解: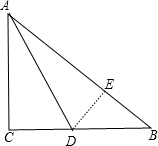 作CE⊥AB于E,如图,
作CE⊥AB于E,如图,
∵AD平分∠BAC,
∴DE=DC,
设CD=x,AC=y,则DE=x,
在Rt△ACD和△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE=y,
∴BE=AB-AE=10-y,
∵∠DBE=∠ABC,
∴Rt△BDE∽Rt△BAC,
∴
=
,即
=
,
∴x=
y,
在Rt△BDE中,
∵DE2+BE2=BD2,
∴x2+(10-y)2=42,
∴(
y)2+(10-y)2=42,
整理得29y2-500y+2100=0,
解得y1=
,y2=10(舍去),
∴x=
×
=
,
在Rt△ABC中,tanA=
=
=
.
 作CE⊥AB于E,如图,
作CE⊥AB于E,如图,∵AD平分∠BAC,
∴DE=DC,
设CD=x,AC=y,则DE=x,
在Rt△ACD和△AED中,
|
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE=y,
∴BE=AB-AE=10-y,
∵∠DBE=∠ABC,
∴Rt△BDE∽Rt△BAC,
∴
| DE |
| AC |
| BD |
| AB |
| x |
| y |
| 4 |
| 10 |
∴x=
| 2 |
| 5 |
在Rt△BDE中,
∵DE2+BE2=BD2,
∴x2+(10-y)2=42,
∴(
| 2 |
| 5 |
整理得29y2-500y+2100=0,
解得y1=
| 210 |
| 29 |
∴x=
| 2 |
| 5 |
| 210 |
| 29 |
| 84 |
| 29 |
在Rt△ABC中,tanA=
| BC |
| AC |
4+
| ||
|
| 20 |
| 21 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了角平分线的性质和相似三角形的判定与性质.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,已知AB=a,BC=b,CE=c,求CF的长.
如图,在?ABCD中,对角线AC、BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,已知AB=a,BC=b,CE=c,求CF的长. 如图,AB=10,BC=6,AC的垂直平分线交AB于D,交AC于E,求△BCD的周长.
如图,AB=10,BC=6,AC的垂直平分线交AB于D,交AC于E,求△BCD的周长.