题目内容
计算或化简
(1)
-
+
;
(2)(x-1)(x-3)-(x-1)2;
(3)解方程:(x-2)2-4=0;
(4)先化简再求值:(a+2b)(2a-b)-(a+2b)2-(a-2b)2,其中a=-
,b=-3.
(1)
| (-3)2 |
| 3 | 8 |
| 4 |
(2)(x-1)(x-3)-(x-1)2;
(3)解方程:(x-2)2-4=0;
(4)先化简再求值:(a+2b)(2a-b)-(a+2b)2-(a-2b)2,其中a=-
| 1 |
| 3 |
考点:整式的混合运算—化简求值,平方根,实数的运算,整式的混合运算
专题:
分析:(1)根据算术平方根和立方根求出每一部分的值,即可得出答案;
(2)先算乘法,再合并即可;
(3)移项后开方,即可得出一元一次方程,求出方程的解即可;
(4)先算乘法,再合并同类项,最后代入求出即可.
(2)先算乘法,再合并即可;
(3)移项后开方,即可得出一元一次方程,求出方程的解即可;
(4)先算乘法,再合并同类项,最后代入求出即可.
解答:解:(1)原式=3-2+2
=3;
(2)原式=x2-3x-x+3-x2+2x-1
=-2x+2;
(3)移项得:(x-2)2=4,
x-2=±2,
x1=4,x2=0;
(4)(a+2b)(2a-b)-(a+2b)2-(a-2b)2
=2a2-ab+4ab-2b2-a2-4ab-4b2-a2+4ab-4b2
=3ab-10b2,
当a=-
,b=-3时,原式=3×(-
)×(-3)-10×(-3)2=-87.
=3;
(2)原式=x2-3x-x+3-x2+2x-1
=-2x+2;
(3)移项得:(x-2)2=4,
x-2=±2,
x1=4,x2=0;
(4)(a+2b)(2a-b)-(a+2b)2-(a-2b)2
=2a2-ab+4ab-2b2-a2-4ab-4b2-a2+4ab-4b2
=3ab-10b2,
当a=-
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查了整式的混合运算,解一元二次方程,算术平方根,立方根等知识点的应用,主要考查学生的计算能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
下列说法中,正确的是( )
| A、正有理数和负有理数统称有理数 |
| B、一个有理数不是整数就是分数 |
| C、零不是自然数,但它是有理数 |
| D、正分数、零、负分数统称分数 |
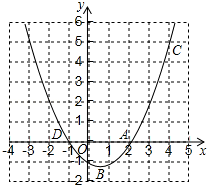 如图,已知二次函数y=ax2+bx+c的图象顶点是(
如图,已知二次函数y=ax2+bx+c的图象顶点是(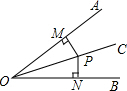 如图,PM=PN,∠BOC=30°,则∠AOB=
如图,PM=PN,∠BOC=30°,则∠AOB=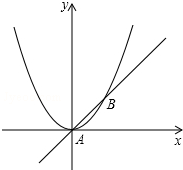 如图,已知直线y=x与抛物线y=x2交于A、B两点.
如图,已知直线y=x与抛物线y=x2交于A、B两点.