题目内容
11. 如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为2$\sqrt{6}$.
如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为2$\sqrt{6}$.
分析 连接AC、OE、OF,作OM⊥EF于M,先求出圆的半径,在RT△OEM中利用30度角的性质即可解决问题.
解答 解;连接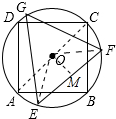 AC、OE、OF,作OM⊥EF于M,
AC、OE、OF,作OM⊥EF于M,
∵四边形ABCD是正方形,
∴AB=BC=4,∠ABC=90°,
∴AC是直径,AC=4$\sqrt{2}$,
∴OE=OF=2$\sqrt{2}$,∵OM⊥EF,
∴EM=MF,
∵△EFG是等边三角形,
∴∠GEF=60°,
在RT△OME中,∵OE=2$\sqrt{2}$,∠OEM=$\frac{1}{2}$∠GEF=30°,
∴OM=$\sqrt{2}$,EM=$\sqrt{3}$OM=$\sqrt{6}$,
∴EF=2$\sqrt{6}$.
故答案为2$\sqrt{6}$.
点评 本题考查正多边形与圆、等腰直角三角形的性质、等边三角形的性质等知识,解题的关键是熟练应用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
6. 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )| A. | 2$\sqrt{2}$<r≤$\sqrt{17}$ | B. | $\sqrt{17}$<r≤3$\sqrt{2}$ | C. | $\sqrt{17}$<r≤5 | D. | 5<r≤$\sqrt{29}$ |
16. 如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )
如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )
 如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )
如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=40°,则∠CAB=( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
3.函数y=$\sqrt{2x-4}$中自变量x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≤2 | D. | x≠2 |
20.$\sqrt{27}$的运算结果应在哪两个连续整数之间( )
| A. | 2和3 | B. | 3和4 | C. | 4和5 | D. | 5和6 |
1. 有两个完全相同的长方体,按如图方式摆放,其主视图是( )
有两个完全相同的长方体,按如图方式摆放,其主视图是( )
 有两个完全相同的长方体,按如图方式摆放,其主视图是( )
有两个完全相同的长方体,按如图方式摆放,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
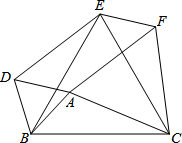 如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.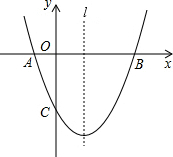 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.