题目内容
1.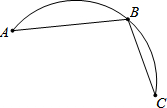 如图是过A,B,C三点的圆弧,
如图是过A,B,C三点的圆弧,(1)作出该圆弧所在圆的圆心(要求尺规作图);
(2)若AB=2,该圆弧所在圆的半径为$\sqrt{2}$,∠ABC=105°,求BC的长.
分析 (1)利用过不在同一直线的三点作圆的方法得出圆心的位置即可;
(2)利用垂径定理得出BD的长,结合勾股定理以及锐角三角函数关系求出BC的长.
解答  解:(1)如图所示:点O即为所求;
解:(1)如图所示:点O即为所求;
(2)如图,∵OD⊥AB,
∴BD=$\frac{1}{2}$AB=1,
又∵OB=$\sqrt{2}$,
∴OD=$\sqrt{O{{B}^{2}-BD}^{2}}$=1,即OD=BD,
∴∠OBD=45°,又∵∠ABC=105°,
∴∠OBC=60°,
∴BE=$\frac{1}{2}$OB=$\frac{\sqrt{2}}{2}$,
∴BC=2BE=$\sqrt{2}$.
点评 此题主要考查了复杂作图以及垂径定理以及勾股定理等知识,正确应用勾股定理得出OD的长是解题关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
9.下列各组数中不能作为勾股数组的是( )
| A. | 6,8,10 | B. | 8,15,17 | C. | 1.5,2,2.5 | D. | 9,12,15 |
16.直线y=x+b与抛物线y=x2+2x+1只有一个公共点,则b的值为( )
| A. | $\frac{5}{4}$ | B. | 1 | C. | $\frac{3}{4}$ | D. | 0 |



