题目内容
在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB于E,若△DBE的周长为4cm,求AB的长.
考点:角平分线的性质,等腰直角三角形
专题:
分析:在△DBE中利用勾股定理可知BD=
BE=
DE,可求得BD和DE,根据角平分线的性质可得CD=DE,可求得BC,再利用勾股定理可求得AB.
| 2 |
| 2 |
解答:解:∵∠C=90°,AC=BC,
∴∠B=45°,
∵DE⊥BE,
∴BD=
BE=
DE,
∵△DBE的周长为4cm,
∴
DE+2DE=4,解得DE=4-2
,
∴BD=4
-4,
∵AD平分∠CAB,
∴CD=DE=4-2
,
∴BC=BD+CD=4
-4+4-2
=2
,
∴AB=
BC=4.
∴∠B=45°,
∵DE⊥BE,
∴BD=
| 2 |
| 2 |
∵△DBE的周长为4cm,
∴
| 2 |
| 2 |
∴BD=4
| 2 |
∵AD平分∠CAB,
∴CD=DE=4-2
| 2 |
∴BC=BD+CD=4
| 2 |
| 2 |
| 2 |
∴AB=
| 2 |
点评:本题主要考查勾股定理和角平分线的性质,掌握角平分线上的点到角两边的距离相等是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
下列各式中,去括号正确的是( )
| A、a+(b-c+d)=a-b+c-d |
| B、a-(b-c+d)=a-b-c+d |
| C、a+(b-c+d)=a-b+c+d |
| D、a-(b-c+d)=a-b+c-d |
 如图是与“杨辉三角”有类似性质的数字三角形表,你能按照发现的规律把这个三角形继续写下去吗?和小伙伴比一比,看谁写得多.试试看.
如图是与“杨辉三角”有类似性质的数字三角形表,你能按照发现的规律把这个三角形继续写下去吗?和小伙伴比一比,看谁写得多.试试看. 如图,BE平分∠ABD,CF平分∠ACD,BE与CF相交于G,若∠BDC=140°,∠BGC=100°,求∠A的度数.
如图,BE平分∠ABD,CF平分∠ACD,BE与CF相交于G,若∠BDC=140°,∠BGC=100°,求∠A的度数.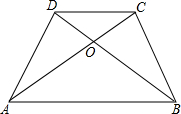 如图,在梯形ABCD中,CD=3,CO:OA=2:3,则AB=
如图,在梯形ABCD中,CD=3,CO:OA=2:3,则AB=