题目内容
11．抛物线y=$\frac{1}{2}{x}^{2}$，y=x2，y=-x2的共同性质是：①都是开口向上；
②都以点（0，0）为顶点；
③都以y轴为对称轴；
④都关于x轴对称．
其中正确的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 利用二次函数的性质，利用开口方向，对称轴，顶点坐标逐一探讨得出答案即可．
解答 解：抛物线y=$\frac{1}{2}{x}^{2}$，y=x2的开口向上，y=-x2的开口向下，①错误；
抛物线y=$\frac{1}{2}{x}^{2}$，y=x2，y=-x2的顶点为（0，0），对称轴为y轴，②③正确；④错误；
故选：B．
点评 本题考查了二次函数的图形与性质；熟记抛物线的开口方向、对称轴、顶点坐标是解决问题的关键．
练习册系列答案
相关题目
1．
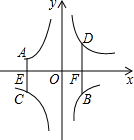如图，A，B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上，C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC=2，BD=3，EF=$\frac{10}{3}$，则k2-k1=（ ）
如图，A，B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上，C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC=2，BD=3，EF=$\frac{10}{3}$，则k2-k1=（ ）| A． | 4 | B． | $\frac{14}{3}$ | C． | $\frac{16}{3}$ | D． | 6 |
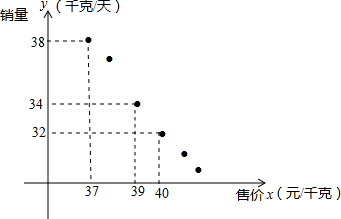某进口专营店销售一种“特产”，其成本价是20元/千克，根据以往的销售情况描出销量y（千克/天）与售价x（元/千克）的关系，如图所示．
如图，已知直线a∥b，△ABC的顶点B在直线b上，∠C=90°，∠1=36°，则∠2的度数是54°．
6．sin30°=（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
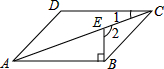如图，在?ABCD中，BE⊥AB交对角线AC于点E，若∠1=20°，则∠2的度数为110°．
如图，图中所有的三角形都是直角三角形，四边形都是正方形，其中最大正方形E的边长为10，则四个正方形A，B，C，D的面积之和为100．